Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 7f
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso.
Passo 1
Fala aí! Nesse exercício daqui estaremos trabalhando a seguinte equação:
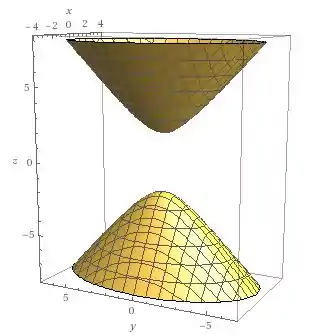
POXA! Eu não sei se você está com as mesmas impressões que eu, mas se estiver, vai estar desconfiado de que esta equação nos representa um hiperboloide, heim? Afinal temos um sendo somado ali. Vamos ver se é isso mesmo?
Passo 2
Podemos aqui, para verificar, levar essa equação para a sua forma clássica: transformar o em e depois jogar todo mundo para um lado só:
Para transformar o em , vamos dividir todo mundo por :
Passando todo mundo que não é para o lado de lá:
AHA!!! Esse é um hiperboloide de folhas ao redor de que tem como definição:
No nosso caso, , e .
Lembre-se de que o paraboloide de duas folhas basta desenhar dois paraboloides, um pra cima e outro pra baixo.
OBS: Repare que ele é achatado em , já que . Além disso, ele tem valores de máximos e mínimos (vértices) em .
Resposta
Paraboloide de 2 folhas ao redor de .
