Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 1.1 - Ex. 3c

(c) C D = [[[d_1,C_1,d_2,C_2,d_3,C_3]]] , em que C_1 = [[[-,2],[0],[-,1]]] , C_2 = [[[1],[1],[0]]] e C_3 = [[[1],[1],[1]]] , são as colunas de C .

Passo 1

Bem galera, nesse exercício precisamos verificar se CD = [ D_1 C_1 D_2 C_2 D_3 C_3 ]. Para descobrirmos se é verdade, precisamos fazer a multiplicação de CD.

O enunciado nos trouxe que C = [ C_1 C_2 C_3 ], e que C_1 , C_2 , C_3 representam colunas da matriz C.

Fazendo a multiplicação vamos ter:

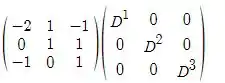
CD =

Vamos então multiplicar as linhas da primeira matriz com as colunas da segunda matriz;

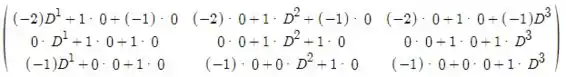
CD =

Agora vamos simplificar a matriz;

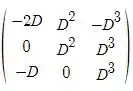
CD =

Passo 2

Bem, agora vamos olhar para a matriz C e compará-la com a matriz CD que acabamos de encontrar.

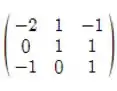
C =CD =

Você conseguiu perceber ?

Elas são equivalentes, podemos então confirmar que está correta a afirmação do enunciado;

CD = [ D_1 C_1 D_2 C_2 D_3 C_3 ].

Podemos perceber que:

D_1 C_1 = D_1 * -2 = -2 D_1

E isso serve para todos os outros elementos.

Resposta

Podemos então confirmar que está correta a afirmação do enunciado

CD = [ D_1 C_1 D_2 C_2 D_3 C_3 ].

Exercícios de Livros Relacionados

Seja A uma matriz nxn . Mostre que se A A t = 0 , então A = 0 . (Sugestão: Use o traço.) E se a matriz A for mxn , com m ≠ n ?
(a)Mostre que se A é uma matriz mxn tal que A X = 0 , para toda matriz X , nx1 , então A = 0 .
Já vimos que o produto de matrizes não é comutativo. Entretanto, certos conjuntos de matrizes são comutativo. Mostre que: (a)Se D 1 e D 2 são matrizes diagonais nxn , então D 1 D 2 = D 2 D 1 .
Seja D = λ 1 0 … 0 0 λ 2 … 0 ⋮ ⋮ ⋱ ⋮ 0 … 0 λ n uma matriz diagonal nxn , isto é, os elementos que estão fora da diagonal são iguais a zero. Seja A = a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ … ⋮ a n 1 a
Dizemos que uma matriz A , nxn , é simétrica se A t = A e é anti-simétrica se A t = - A . (e)Mostre que para toda matriz A ,nxn ,A + A t é simétrica e A - A t é anti-simétrica.