Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 2.Exercícios Propostos - Ex. 9

No Δ A B C temos A B   → =   b →   , A C   → =   c →   , 3 A P   → =   2 P C →   e B Q   → = λ   B C →   . Determine λ →   para que P Q → fique paralelo ao vetor 2 A B   → +   A C →   +   B C → .

Passo 1

Olá! Animado para mais uma resolução? Então vamos lá! Vamos começar desenhando um triângulo com todas as informações do enunciado.

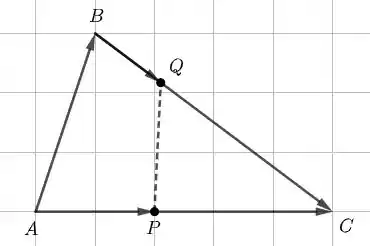
Primeiramente, vamos escrever P Q → em termos de A B , →   A C → ,   B C → :

P Q → = P C → + C Q → = P C → - Q C →

Segundamente, temos que notar que

B Q   → = λ   B C → = λ ( B Q → + Q C → ) ⇒ Q C → = ( 1 - λ ) λ B Q   → = ( 1 - λ ) λ λ   B C → = ( 1 - λ )   B C →

A C → = A P → + P C → = 2 3 P C → + P C → = 5 3 P C → ⇒ P C → = 3 5 A C → = 3 5 c →

Como B C → = B A → + A C → = -   b → + c → , então,

Q C → = ( 1 - λ )   B C → = ( 1 - λ ) ( -   b → + c → )

Agora, voltamos ao vetor P Q → :

P Q → = P C → - Q C → = 3 5 c → - ( 1 - λ ) ( -   b → + c → ) = ( 1 - λ )   b → + ( λ - 2 5 ) c →

Passo 2

Calma que essa foi só a primeira parte. Agora temos que obter 2 A B   → +   A C →   +   B C → , mas isso é fácil:

2 A B   → +   A C →   +   B C → = 2 A B   → +   A C →   + B A → + A C → = 2   b →   +   c → -   b → +   c → =   b →   + 2   c →

Essa parte foi tranquila, agora podemos finalmente resolver a questão.

Passo 3

Para determinar λ →   de modo que P Q → fique paralelo ao vetor 2 A B   → +   A C →   +   B C → temos que fazer

P Q → = α ( 2 A B   → +   A C →   +   B C → )

O vetor P Q → foi obtido no Passo 1 e o vetor 2 A B   → +   A C →   +   B C → no Passo 2, então só precisamos substituir os resultados na equação acima

( 1 - λ )   b → + ( λ - 2 5 ) c → = α (   b →   + 2   c → ) ⇒ ( 1 - λ - α )   b → = ( 2 α + 2 5 - λ )   c →

Como b → e   c → não são paralelos, a equação acima só é verdadeira se ambos os lados forem nulos. Assim, devemos ter

1 - λ - α = 0 ⇒ λ = 1 - α

2 α + 2 5 - λ = 0 ⇒ 2 α + 2 5 - 1 + α = 0 ⇒ 3 α - 3 5 = 0 ⇒ α = 1 5

⇒ λ = 1 - α = 1 - 1 5 = 4 5

Resposta

λ = 4 5

Exercícios de Livros Relacionados

Prove: o espaço gerado por dois vetores em R 3 é uma reta pela origem, um plano pela origem, ou a própria origem.
Mostre que se { v 1 ,v 2 } for um conjunto linearmente independente e se v 3 não pertencer a g e r v 1 ,v 2 , então { v 1 ,v 2 ,v 3 } é linearmente independente.
Os vetores v 1 , v 2 e v 3 na parte (a) da figura dada são linearmente independentes? E os da parte (b)? Explique.
Utilizando identidades apropriadas, onde necessário, determine quais dos conjuntos de vetores em F ( - ∞ ,∞ ) dados são linearmente dependentes.f) 0 , cos 3 ⁡ π x , sen ⁡ 3 π x
Utilizando identidades apropriadas, onde necessário, determine quais dos conjuntos de vetores em F ( - ∞ ,∞ ) dados são linearmente dependentes.d) cos ⁡ 2 x , sen 2 ⁡ x , cos 2 ⁡ x