Exercícios de Combinação e Dependência Lineares - Lista de Exercícios Resolvida

Verificar se o conjunto do é ou .

Sabendo que , ,   , determine   sabendo que  ,   e   estão no mesmo plano.

Determinar o valor de  para que o vetor   seja combinação linear de e  .

Determine, para cada um dos itens abaixo, se é combinação linear de e :

Prove que, se um conjunto de vetores for , podemos escrever um dos vetores como combinação linear dos demais.

Determinar o valor de para que o conjunto seja .

Escreva o vetor como combinação linear dos vetores

e

e

Consideremos no os seguintes vetores:   e  

1. Escrever o vetor   como combinação linear de   e  
2. Mostrar que o vetor   não é combinação linear de   e  

Quais dos seguintes conjuntos de vetores em são linearmente dependentes?

(a)

(b)

(c)

Se então, necessariamente:

(I) O conjunto é linearmente dependente.

(II) não pertence ao conjunto gerado por e .

(a) I é verdadeira e II é verdadeira.

(b) I é falsa e II é verdadeira.

(c) I é falsa e II é falsa.

(d) I é verdadeira e II é falsa.

São dados três pontos não colineares , e e, sobre o segmento o ponto tal que . Escreva como combinação linear de e .

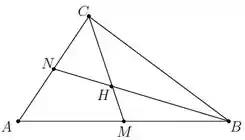
Considere três pontos não colineares , e , o ponto médio do segmento , , o ponto médio do segmento , , e o ponto comum aos segmentos e , .

a) Escreva como combinação linear de e .

b) Escreva como combinação linear de e .

c) Mostre que e .

Seja um conjunto linearmente independente e uma combinação linear de e .

(I) e não podem ser ambos linearmente independentes.

(II) e podem ser ambos linearmente dependentes.

(a) I é verdadeira e II é falsa

(b) Ambas são verdadeiras

(c) I é falsa e II é verdadeira

(d) Ambas são falsas