Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 15.Exercício - Ex. 11

O triângulo A B C é retângulo em B e está contido em π 1 : x + y + z = 1 . O cateto B C está contido em π 2 : x - 2 y - 2 z = 0 e a hipotenusa mede 2 6 3 . Sendo A = ( 0 ,   1 ,   0 ) , determine B e C (o sistema de coordenadas é ortogonal).

Passo 1

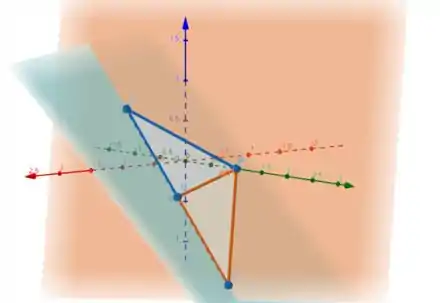
Pelos dados do exercício, a imagem que temos é mais ou menos isso aqui:

Onde o plano laranja é π 1 , o plano azul é π 2 e queremos descobrir os pontos B e C .

Os pontos B e C vão estar na reta da intersecção dos planos, vamos encontrar essa reta pelo sistema:

x + y + z = 1 - x + 2 y + 2 z = 0

Somando as duas equações:

3 y + 3 z = 1

y = - z + 1 3

Substituindo na primeira equação:

x - z + 1 3 + z = 1

x = 2 3

Então a reta vai ser dada por:

x ,   y ,   z = 2 3 ,   - z + 1 3 ,   z

Transformando z no parâmetro λ , temos a reta:

r :   x ,   y ,   z = 2 3 , 1 3 ,   0 + λ ( 0 ,   - 1 ,   1 )

Passo 2

Sabemos que o ponto C está na reta r certo?

Então ele pode ser escrito de uma forma genérica:

C = 2 3 , 1 3 - λ ,   λ

Sabemos que o vetor A C → , hipotenusa do triângulo, deve medir 2 6 3 . Temos que:

A C → = C - A = 2 3 ,   - 2 3 - λ ,   λ

Calculando o módulo de A C → e igualando a 1 3 :

A C → = 2 3 2 + - 2 3 - λ 2 + λ ² = 2 6 3

Resolvendo essa equação, encontramos λ ' = 2 3 e λ ' ' = - 4 3 , então os possíveis pontos C são:

C ' = 2 3 ,   - 1 3 , 2 3

C ' ' = 2 3 , 5 3 ,   - 4 3

O que nos dá algo parecido com isso:

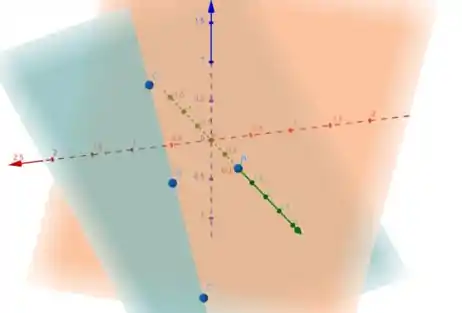
Passo 3

Agora precisamos achar o ponto B , mas epa, se o triângulo é retângulo, ele com certeza está no ponto médio entre os dois valores possíveis de C , então:

B = 2 3 ,   - 1 3 , 2 3 + 2 3 , 5 3 , - 4 3 2 = 4 3 , 4 3 ,   - 2 3 2 = 2 3 , 2 3 ,   - 1 3

Então, temos essas duas possibilidades de triângulo retângulo:

Resposta

B = 2 3 , 2 3 ,   - 1 3

C ' = 2 3 ,   - 1 3 , 2 3

C ' ' = 2 3 , 5 3 ,   - 4 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam A = 1 ,4 ,0 e B = 0 ,1 ,- 2 . Nos casos do exercício anterior, obtenha equações do lugar geométrico dos pontos médios dos segmentos paralelos a A B com uma extremidade em π 1 e outra em π 2 . De
Seja A = 1,4 , 0 e B = 0,1 , - 2 . Nos casos do exercício anterior, obtenha equações do lugar geométrico dos pontos médios dos segmentos paralelos a A B com uma extremidade em r e outra em π . Descrev
Seja A = 1,4 , 0 e B = 0,1 , - 2 . Nos casos do exercício anterior, obtenha equações do lugar geométrico dos pontos médios dos segmentos paralelos a A B com uma extremidade em r e outra em π . Descrev
Seja A = 1,4 , 0 e B = 0,1 , - 2 . Nos casos do exercício anterior, obtenha equações do lugar geométrico dos pontos médios dos segmentos paralelos a A B com uma extremidade em r e outra em π . Descrev
Sejam A = 1,0 , 0 , B = 0,2 , 0 , C = 0,0 , 3 e O = 0,0 , 0 . Obtenha uma equação geral do plano paralelo ao plano A B C que intercepta as retas O A , O B e O C em pontos que são vértices de um triâng