Análise da Multiplicação de Matrizes
Produzido por Bruno PestanaTeoria
Intervalo de Confiança para Diferença entre Proporções
Em “Operações com Matrizes” vimos uma maneira de fazer a multiplicação entre matrizes. E se eu te disser que existe outra forma de visualizar essa operação?
Isso mesmo, existe outro jeito de interpretar a multiplicação de matrizes! Alguns professores nem falam dela, mas tem muitas questões que saem muito mais facilmente dessa forma (algumas só dessa forma :p).
Se tivermos a matriz abaixo:
Formada pelos vetores coluna e . E multiplicarmos por uma matriz , por exemplo:
Podemos fazer o seguinte:
Percebeu o que aconteceu? Combinamos as colunas de usando os elementos das colunas de como coeficientes! Olha esse exemplo:
O mesmo resultado né (ufa haha). No fundo estamos fazendo o mesmo que fizemos lá no produto que aprendemos. Só que lá fizemos termo a termo e aqui estamos fazendo coluna por coluna.
A última forma que temos para ver esse produto é como uma combinação das linhas de ! Como assim? Se liga, agora vamos ter
E o produto vai ficar:
Ou seja, estamos combinando as linhas de usando os elementos das linhas de como coeficientes. Aplicando no nosso exemplo:
De novo deu o mesmo resultado! Ent��o a mensagem que eu queria passar para vocês é que o produto pode ser entendido como a combinação linear das colunas de , ou como a combinação linear das linhas de !
Resumindo as três formas de multiplicar que a gente viu (que na verdade são a mesma forma):
Obs.: Agora que sabemos multiplicar matrizes por matrizes, ou mais especificamente, por vetores (se a matriz tiver apenas coluna), podemos perceber que a matriz “pegará” vetores do e levará em vetores do . Por exemplo se temos uma matriz :
Ela leva vetores do em vetores do !
Propriedades de Multiplicação de Matrizes
Além disso, existem algumas propriedades que partem da multiplicação de matrizes que é bom dar uma olhada:
1) (o produto de matrizes é associativo)
2)
3)
4)
OBS1: Em relação ao número 2 e 3, Podemos perceber que o LADO no qual multiplicamos a matriz importa e muito. No caso 2, não poderíamos botar em evidência a matriz à direita pois o resultado ficaria diferente, já que, em geral, e ! Chamamos o caso 2 de botar em evidência à esquerda.
OBS2: O mesmo vale para o caso 3, onde podemos perceber que botar em evidência à direita é diferente de botar em evidência à esquerda, já que, em geral, e .
Propriedades de Multiplicação de Matrizes
Exercícios Resolvidos
Exercício Resolvido #1
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 127 – Fix. 4.16
Qual(is) das seguintes propriedades do produto de matrizes são validas?
Associatividade?
Comutatividade?
Distributividade?
Passo 1
Letra
Associatividade é você poder associar do jeito que você quiser:
Logo a primeira é verdade.
Letra
A comutatividade é falsa, pois sabemos que a ordem do produto de matrizes importa.
Letra
Essa é um pouco confusa. Mesmo que a distributividade de matrizes seja meio zoado, dizemos que ela é distributiva sim:
Resposta
Associatividade
Distributividade
Exercício Resolvido #2
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 127 – Fix. 4.17
Se então _______
Passo 1
Lembrando que o produto das matrizes é distributivo, mas com aquela restrição de qual lado você está multiplicando. Se chamarmos pra ficar mais fácil de visualizar, temos:
Substituindo de volta:
Sendo assim, podemos ver que a resposta é a segunda opção.
Resposta
Exercício Resolvido #3
Anton e Rorres, Álgebra Linear com Aplicações, 8ª Ed., Porto Alegre, Bookman, 2005, pp. 47 – ex. 9
Sejam
e
Mostre que o produto pode ser expresso como uma combinação linear das matrizes-linha de com coeficientes escalares vindo de
Passo 1
Bom, pra começar, vamos organizar isso aí, queremos , que vou chamar de :
Agora temos que achar esses elementos de para mostrar que esse vetor é uma combinação linear das linhas de com os elementos do vetor como coeficientes:
Vamos tentar escrever isso aí como uma combinação linear, ou seja, uma expressão de vetores, de um lado vamos ter:
Para escrever o outro lado, precisamos analisar essas expressões dos , vemos que o primeiro termo de todas elas é composta por multiplicado por um termo da primeira linha da matriz , então o primeiro termo da nossa vai ser:
E o mesmo vai acontecer com os outros termos, que vão ser:
Juntando tudo:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
UFRJ, Álgebra Linear, P1 – 2015.1, Questão 06
Sejam e duas matrizes cujo produto é a matriz nula, isto é, . Pode-se afirmar que:
O conjunto das linhas de é linearmente dependente ou o conjunto das colunas de é linearmente dependente.
O conjunto das colunas de é linearmente dependente ou o conjunto das linhas de é linearmente dependente.
ou
Passo 1
Vamos começar de traz pra frente essa questão?! Confia em mim!!! Podemos descartar logo de cara os itens (c) e (d). Vamos ver o porquê?!
O item (c) não é verdadeiro porque a multiplicação de matrizes não é comutativa, então se não há garantias que seja zero também.
O item (d) podemos interpretar da seguinte forma : Se então ou . Note que, se e , então a matriz teria que ser a matriz identidade (que é o elemento neutro da multiplicação), porém a matriz não é uma matriz quadrada, logo não é a matriz identidade. Podemos pensar a mesma coisa na situação inversa com e .
Então, concluímos que ambas são falsas. Beleza?!
Passo 2
Vamos analisar os itens (a) e (b) como uma coisa só. Precisamos checar qual fator irá influenciar no produto , as linhas ou colunas de A
Vamos pensar no que fazemos quando multiplicamos matrizes!
Nós podemos combinar as colunas de , ou combinar as linhas de .
Essa primeira interpretação é a mais usual. Nós usamos os vetores coluna de para combinar as colunas de . vamos pegar uma matriz onde suas colunas são (todas as colunas forem uma combinação linear entre si). Por exemplo:
Temos que
Ou seja, já vimos que podemos zerar qualquer matriz com colunas .
Passo 3
A outra interpretação é um pouco mais chatinha de ver já que não estamos acostumados. Vamos usar uma matriz com linhas (linearmente dependentes) dessa vez, ou seja, todas as linhas de B são combinações lineares entre si. Por exemplo:
O produto ficaria:
Para fazer a multiplicação podemos pegar a primeira coluna de e combinar as colunas de com esses coeficientes:
Essa é a primeira coluna de certo? Esse é o método que já conhecemos. Outra forma é pegarmos a primeira linha de e combinar as linhas de com esses coeficientes:
E essa é a primeira linha de !
Então, se possui colunas ou se possui linhas , podemos zerar o produto ;)
Resposta
Letra
Exercício Resolvido #5
UFRJ, Álgebra Linear, P1 – 2015.1, Questão 05
Seja uma matriz . Deseja-se construir uma matriz de forma que o produto seja uma matriz satisfazendo:
A primeira linha de é igual à metade da soma de todas as linhas de ;
A segunda linha de é igual à metade da diferença entre as duas últimas linhas de ;
A terceira linha de é igual à primeira linha de ;
Qual a soma de todos os elementos da matriz ?
Passo 1
Antes de mais nada vamos nos organizar!!
Primeiro vamos ver o tamanho de . Temos o seguinte:
Assim, para que o produto seja possível, precisamos que o número de colunas de seja igual ao número de linhas de , logo .
Como terá o número de linhas de e o número de colunas de , para que seja precisamos que .
Entãojá sabemos que é uma matriz . Beleza?!
Passo 2
Normalmente nós faríamos o produto combinando as colunas de usando os elementos das colunas de como coeficientes, mas esse método não serve pra nada aqui!!
Por sorte, também sabemos que o produto pode ser entendido como uma combinação das linhas de usando os elementos das linhas de como coeficientes! Esse é o tipo de questão que fica muuuuito mais fácil de resolver sabendo isso, como eu comentei na teoria haha. Vamos lá então:
O enunciado nos diz que a primeira linha de é igual à metade da soma de todas as linhas de .
Então a primeira linha de tem que somar metade de todas as linhas de , logo todos os elementos dessa linha vão ser :
Passo 3
A segunda linha de é igual à metade da diferença entre as duas últimas linhas de .
Portanto, a segunda linha de tem que fazer a diferença das metades das duas últimas linhas de . Beleza?! O primeiro elemento dessa linha será nulo pois ele acompanha a primeira linha de na combinação, assim:
Passo 4
A terceira linha de é igual à primeira linha de .
Nesse caso teremos que zerar os 2 últimos elementos dessa linha, pois remetem a segunda e terceira linha de . Então a terceira linha de é:
Passo 5
Queremos a soma de todos os elementos da matriz , então é só somar todos os elementos de hahahahahaha:
Resposta
Letra
Exercício Resolvido #6
FAAP - SP
Uma montadora produz três modelos de veículos: , e . Neles podem ser instalados dois tipos de airbags: e . A matriz mostra a quantidade de unidades de airbags instaladas
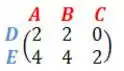
Numa determinada semana, foram produzidas as seguintes quantidades de veículos, dadas pela matriz :
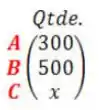
O produto da matriz pela matriz é .
Quantos veículos do modelo foram montados na semana?
a) 300
b) 200
c) 150
d) 0
e) 100
Passo 1
Ok, vimos que o produto entre a matriz pela matriz é igual a , ou seja:
E nós queremos encontrar o valor de , que é a quantidade de veículos no modelo belezinha? Pra isso vamos fazer a multiplicação das matrizes.
Passo 2
Multiplicando as matrizes:
Agora é só somar essas matrizes
Igualando os termos :
Ou seja, foram produzidas veículos do modelo . Logo, a alternativa correta é a letra B!!
Resposta
b) 200
Exercício Resolvido #7
UF - AM
Sendo
,
E . Então a matriz é igual a:
a)
b)
c)
d)
e)
Passo 1
Vamos lá, sabemos que , ou seja:
Para que seja possível realizar o produto , como tem colunas, deve ter 2 linhas certo?
Para que a multiplicação de uma matriz com resulte em uma matriz , a matriz deve ter apenas coluna (lembrando: a matriz resultado de um produto entre matrizes, vai ter a quantidade de linhas da primeira matriz e a quantidade de colunas da segunda).
Então vai ser uma matriz (vamos fingir que não vimos isso nas alternativas haha).
Passo 2
Agora, vamos realizar o produto entre e daquele jeitinho que vimos na teoria para encontrarmos os valores de e , que formam nossa matriz :
Somando as matrizes:
Ok, então temos que
Passo 3
Vamos multiplicar a equação por , isso vai nos dar
Agora vamos somar as equações e :
Substituindo o valor de na equação (poderia ser na também):
Ebaaa! Encontramos o valor de e :D
Enfim, a nossa matriz então é:
Logo, a alternativa correta é a letra C!!
Resposta
c)
Exercício Resolvido #8
PUC - RS
Sendo
,
E , o elemento da matriz é:
a) 9
b) 0
c) -4
d) -8
e) -12
Passo 1
Vimos que a matriz é o produto . Para descobrirmos o elemento , precisamos realizar o produto dessas matrizes. Que tal resolvermos do jeito que vimos na teoria? Fica assim:
Passo 2
Multiplicando as matrizes coluna pelos escalares, vamos ter
Agora é só somar :)
Então nossa matriz é
Passo 3
Queremos o elemento , ou seja, o elemento de que está na terceira linha e terceira coluna. No caso, é o certo? Logo, a alternativa correta é a letra d :D
Resposta
d) -8