Exercícios de Análise da Multiplicação de Matrizes - Lista de Exercícios Resolvida

Sejam e duas matrizes cujo produto é a matriz nula, isto é, . Pode-se afirmar que:

O conjunto das linhas de é linearmente dependente ou o conjunto das colunas de é linearmente dependente.

O conjunto das colunas de é linearmente dependente ou o conjunto das linhas de é linearmente dependente.

ou

Sejam

e

Mostre que o produto pode ser expresso como uma combinação linear das matrizes-linha de com coeficientes escalares vindo de

Se então _______

Sendo

,

E , o elemento da matriz é:

a) 9

b) 0

c) -4

d) -8

e) -12

Uma montadora produz três modelos de veículos: , e . Neles podem ser instalados dois tipos de airbags: e . A matriz mostra a quantidade de unidades de airbags instaladas

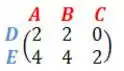
Numa determinada semana, foram produzidas as seguintes quantidades de veículos, dadas pela matriz :

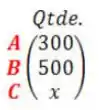
O produto da matriz pela matriz é .

Quantos veículos do modelo foram montados na semana?

a) 300

b) 200

c) 150

d) 0

e) 100

Sendo

,

E . Então a matriz é igual a:

a)

b)

c)

d)

e)

Seja uma matriz . Deseja-se construir uma matriz de forma que o produto seja uma matriz satisfazendo:

A primeira linha de é igual à metade da soma de todas as linhas de ;

A segunda linha de é igual à metade da diferença entre as duas últimas linhas de ;

A terceira linha de é igual à primeira linha de ;

Qual a soma de todos os elementos da matriz ?

Qual(is) das seguintes propriedades do produto de matrizes são validas?

Associatividade?

Comutatividade?

Distributividade?

Sejam , e tal que e . Calcule a primeira coluna da matriz A:

(a)

(b)

(c)

(d)

39) Prove: se , então é simétrica e .

4. Seja uma matriz com a propriedade que . Escolha a alternativa FALSA

(a) não é inversível

(b) Os autovalores de são e

(c) A solução de é

(d) é inversível e

(e) Não sei.

Sejam , e tal que e Calcule a segunda coluna da matriz

Seja uma matriz qualquer:

I - Pode-se afirmar que existe apenas um vetor tal que é igual à soma de todas as colunas de

II - Não existe nenhum vetor tal que é igual à diferença entre a primeira e a última colunas de A

(a) I é verdadeira e II é falsa

(b) Ambas são verdadeiras

(c) I é falsa e II é verdadeira

(d) Ambas são falsas

Seja uma matriz . Deseja-se construir uma matriz tal que o produto seja uma matriz satisfazendo as condições abaixo:

i. A primeira linha de deve ser igual à diferença entre as linhas de ;

ii. A segunda linha de deve ser igual ao dobro da soma das linhas de e

iii. A terceira linha de deve ser igual ao dobro da primeira linha de menos a segunda linha de A.

A soma de todos os elementos da matriz é:

(a) 5

(b) 3

(c) 0

(d) 6

Seja C uma matriz tal que o sistema tem solução única. Considere as afirmações.

(I) É possível que C seja um produto de matrizes C = AB onde A é e B é

(II) É possível que C seja um produto de matrizes C = AB onde A é e B é

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Sejam e matrizes tais que o produto matricial está definido. Considere as seguintes afirmações:

As colunas do produto são combinações lineares das colunas de .

As linhas do produto são combinações lineares das linhas de

Qual das opções abaixo é CORRETA?

A afirmativa é falsa e é falsa.

A afirmativa é falsa e é verdadeira.

A afirmativa é verdadeira e é falsa.

A afirmativa é verdadeira e é verdadeira.

Sejam e matrizes tais que Assinale abaixo a matriz de forma que a primeira linha de seja igual à soma das linhas de a segunda linha de seja igual à diferença entre as linhas de e a terceira linha de seja igual à segunda linha de Assinale a soma dos elementos da segunda coluna de

a)

b)

c)

d)

Sejam A e B duas matrizes. Considere as afirmações.

(I) Se o produto AB está definido, então o produto BA também está.

(II) Se os produtos AB e BA estão definidos, então A e B são quadradas.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é falsa e (II) é verdadeira.

Seja uma matriz . Deseja-se construir uma matriz de forma que o produto seja uma matriz satisfazendo:

A primeira coluna de é igual a soma das colunas de ;

A segunda coluna de é igual à diferença entre as colunas de ;

Qual a soma de todos os elementos da matriz ?

Deseja-se construir uma matriz de forma que o produto seja uma matriz satisfazendo as condições abaixo, qualquer que seja a matriz .

A primeira linha de deve ser igual à soma das linhas de .

A segunda linha de deve ser igual à diferença entre as linhas de e

A terceira linha de deve ser igual ao triplo da primeira linha de menos o dobro da segunda linha de .

Qual é a soma de todos os elementos da matriz ?

Sejam e duas matrizes cujo produto é a matriz nula, isto é, . Pode-se afirmar que:

O conjunto das linhas de é linearmente dependente ou o conjunto das colunas de é linearmente dependente.

O conjunto das colunas de é linearmente dependente ou o conjunto das linhas de é linearmente dependente.

ou