Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Operações com Matrizes

Ver Todos os Exercícios

Teoria

Fala aí, nós somos o Responde Aí, e estamos aqui com você hoje para falarmos sobre as operações com matrizes. Bora lá ✌🏾

Nós vamos separar as operações e falar com calma de cada uma delas belezinha?

Soma e Subtração

Quando queremos somar ou subtrair matrizes o que temos que fazer é soma ou subtrair elemento com elemento, ou seja, o primeiro termo de uma matriz soma ou subtraído do primeiro termo da outra matriz.

Dá uma olha nesse exemplo aqui:

Vamos fazer dessa forma aqui:

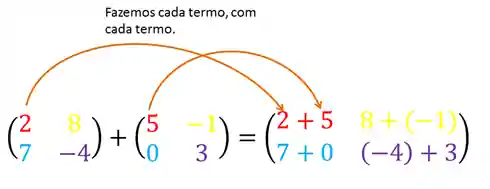
Se fizermos essas continhas para cada termo temos o resultado da soma de matrizes:

Só uma coisa bem importante, que você deve tomar muito cuidado: Paraa somar ou subtrair matrizes, elas precisam ter a mesma quantidade de linhas e colunas.

Multiplicação de uma matriz por um número

Essa operação aqui é bem tranquila. Para multiplicar a matriz por um número, basta você multiplicar todos os elementos da matriz por esse número.

Se liga nesse exemplo:

O número vai "entrar" na matriz multiplicando cada termo:

A ideia é a mesma para qualquer que seja a quantidade de colunas e linhas da nossa matriz.

Multiplicação entre matrizes

Essa é a operação mais importante e é um pouco mais complexa que as que a gente já viu aqui, mas não precisa se desesperar. Só vem comigo 😉

Primeiro de tudo, para a gente conseguir fazer a multiplicação entre duas matrizes, é necessário que o número de colunas da primeira matriz seja igual a número de linhas da segunda matriz. E a matriz que obteremos como resultado terá o número de linhas da primeira e o número de colunas da segunda:

Onde:

  • , matriz , com linhas e colunas;
  • , matriz , com linhas e colunas, e;
  • , matriz , com linhas e colunas;

IMPORTANTÍSSIMO: Na operação de multiplicação entre matrizes a ORDEM IMPORTA, ou seja, é diferente de . É necessário ficar muito atento a isso e a quantidade de linhas e colunas de cada matriz para verficar se a operação pode ser feita ou não.

Beleza, mas como fazar a multiplicação? Para isso, você precisa guardar essa frase aqui no coração: "LINHA POR COLUNA"

O que essa frase quer dizer? Você vai pegar a primeira linha da matriz e multiplicar ela pela primeira coluna de , depois pela segunda coluna de , até acabarem as colunas de . Depois, você vai pegar a segunda linha da matriz e multiplicar ela pela primeira coluna de , depois pela segunda coluna de , até acabarem as colunas de . E assim por diante, até acabar a matriz toda.

Meio confuso? Calma, vamos para o exemplo

Olha essas matrizes aqui:

Primeiro temos que ver o número de linhas e colunas. A matriz tem colunas e a matriz tem linhas, então podemos multiplicá-las.

Agora, vamos multiplicar a primeira linha de com a primeira coluna de :

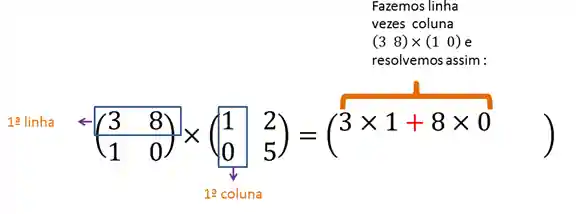
Agora, continuando na primeira linha da matriz A, vamos multiplicar pela segunda coluna de B:

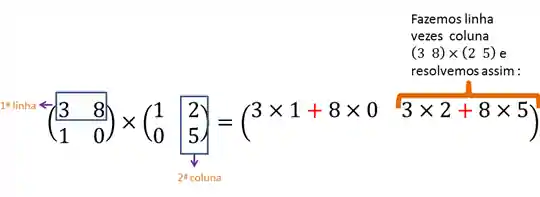
Terminamos a primeira linha da matriz resultante, vamos para a segunda linha de com a primeira coluna de :

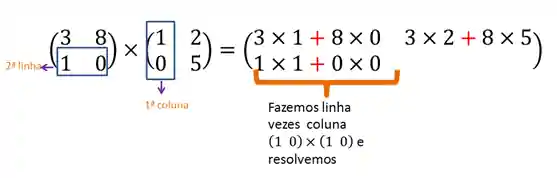
Para finalizar, vamos pegar a segunda linha de com a segunda coluna de :

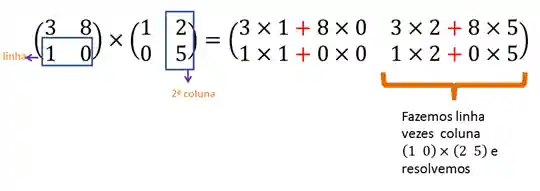
Agora é só resolver a expressãozinha para cada termo da matriz e obtemos o seguinte resultado:

Prontinho!!

Propriedades da multiplicação de matrizes

Existem três propriedades da multiplicação entre matrizes bem importanteS. Eu vou colocar elas aqui em um quadrinho para você:

Multiplicação de uma matriz por um número

Multiplicação entre matrizes

Propriedades da multiplicação de matrizes

Exercícios Resolvidos

Exercício Resolvido #1

Miguel Jorge, Thales do Couto, Felipe da Silva, Ralph Teixeira., Matemática para o Ensino Médio – volume II , Rio de Janeiro, Editora brasil, Página 260, 2010 exemplo IV

Seja A = 1 2 3 3 1 0 e B = 1 0 0 0 1 0 0 0 1 , calcule A B .

Passo 1

Bom esta questão da pra resolver sem fazer conta!

Primeiro de tudo, como A 2 × 3 e B 3 × 3 , podemos multiplicar e a nova matriz será 2 × 3 .

Passo 2

Você pode tentar calcular do jeito normal, mas lembre-se que essa matriz B é a identidade! E como propriedade temos que qualquer matriz multiplicada pela identidade é ela mesma logo, A B = A .

Resposta

A B = A .

Exercício Resolvido #2

Miguel Jorge, Thales do Couto, Felipe da Silva, Ralph Teixeira., Matemática para o Ensino Médio – volume II , Rio de Janeiro, Editora brasil, Página 260, 2010, exemplo ii

Dadas as matrizes A = 1 2 3 2 0 1 e B = 2 - 1 0 3 1 2 , calcular A B .

Passo 1

Primeira coisa: vamos ver se dá para multiplicar as matrizes. Como A 2 × 3 e B 3 × 2 , é possível efetuar a multiplicação. Então podemos perceber que ao fazermos A B obtemos A B = C 2 × 2 .

Passo 2

Vamos efetuar a multiplicação lembre-se basta multiplicar as colunas de B pelas linhas de A :

A primeira coluna de C é:

a 11 = 1.2 + 2.0 + 3.1 = 5

a 21 = 2.2 + 0.0 + 1.1 = 5

Passo 3

A segunda coluna de C é:

a 12 = 1 . - 1 + 2.3 + 3.2 = 11

a 22 = 2 . - 1 + 0.3 + 1.2 + 0

Resposta

C = a 11 a 12 a 21 a 22 = 5 11 5 0

Exercício Resolvido #3

UFRJ, Álgebra Linear, P1, 2014.2, Questão 8

Existe apenas uma ordem de se fazer o produto das 3 matrizes abaixo:

A = 2 - 2 4 1 ,   B = 2 1 1   e   C = 2 - 2 4 2 - 2 4

Descubra qual a ordem dos fatores, multiplique-os e assinale o resultado correto:

( a ) 4 2 2 2 1 1 2 1 1

( b ) 4 - 4 8 2 - 4 4 - 8 - 2 8 - 8 16 4 2 - 2 4 1

( c ) 12 - 12 24 6 12 - 12 24 6

( d ) 6 6

Passo 1

Bom, sabemos que para multiplicar matrizes elas tem que se “encaixar” certinho. Temos que achar a única forma que essas três aí se encaixam. Vamos ver:

A 1 × 4 ,   B 3 × 1   e   C 2 × 3

O jeito mais fácil é procurarmos a matriz que vai ficar no meio! Ela tem que ter o número de linhas igual o número de colunas de alguma matriz. E também tem que ter o número de colunas igual ao número de linhas da outra matriz que sobrou. Analisando isso chegamos na matriz B ! Se liga:

C 2 × 3 ⏟ ∙ B 3 ⏟ × 1 ⏞ ∙ A 1 ⏞ × 4

Passo 2

Beleza, agora a gente podia seguir a sugestão do enunciado e multiplicar as matrizes, mas como não podemos ficar perdendo tempo de prova vamos ser espertos e perceber que a matriz resultante será 2 × 4 !! Para vermos isso, é só pegarmos os números que ficaram nas pontas do produto:

C 2 ⏟ × 3 ∙ B 3 × 1 ∙ A 1 × 4 ⏟

A única resposta com matriz 2 × 4 é a da letra c então matamos a questão aí.

Resposta

Letra ( c )

Exercício Resolvido #4

José Luiz Boldrini, Sueli I. Rodrigues Costa, Vera Lúcia Figueiredo e Henry G. Wetzler, Álgebra Linear, 3 a ed. Rio de Janeiro, HARBRA, 1980, pp. 13 – 2.

Seja A = 2 x 2 2 x - 1 0 . Se A T = A , então x = _ _ _ _ _ _ _ _ _ _ .

Passo 1

Bom, o primeiro passo é achar a matriz transposta, ou seja, trocar as linhas e colunas de lugar.

A T = 2 2 x - 1 x 2 0

Passo 2

Agora vamos igualar as matrizes. Para elas serem iguais é preciso que todos os seus respectivos elementos sejam iguais.

A T = A

2 x 2 2 x - 1 0 = 2 2 x - 1 x 2 0

Vamos igualar elemento por elemento:

2 = 2

2 x - 1 = x 2

x 2 = 2 x - 1

0 = 0

A primeira e a última equação são bem obvias hahaha, então vamos dar uma olhada nas duas do meio. Opa, elas são iguais, facilitou muita coisa!!

Passo 3

Vamos resolver a equação para acharmos o x :

2 x - 1 = x 2   ⇒   x 2 - 2 x + 1 = 0

x = 2 ± 4 - 4 2 = 1

Resposta

x = 1

Exercício Resolvido #5

Instituto Federal Catarinense, Lista de Álgebra Linear, Marcelo Cendron, Curso de Engenharia de Controle e Automação - Adaptado

Determine os valores de a , b , c e d :

A = a 3 - 1 a + b = 4 d - 2 c d + 2 c - 2

Passo 1

Vamos igualar cada elemento da mesma linha e coluna nas duas matrizes dadas:

a = 4   ( i )

3 = d - 2 c   ( i i )

- 1 = d + 2 c   ( i i i )

a + b = - 2   ( i v )

Belezinha, na equação ( i ) já temos o valor de a :) agora bora encontrar o restante!!

Passo 2

Substituindo ( i ) em ( i v ) :

4 + b = - 2

b = - 6

Agora só falta c e d !!

Passo 3

Vamos somar as equações ( i i ) e ( i i i ) :

3 + - 1 = d - 2 c + d + 2 c

2 = 2 d

d = 1

Substituindo o valor de d na equação ( i i ) :

3 = 1 - 2 c

2 c = 1 - 3

2 c = - 2

c = - 1

Isso aí!! Achamos todos!! :D

Resposta

a = 4

b = - 6

c = - 1

d = 1

Exercício Resolvido #6

Matematiquês – Lista de Matrizes, determinantes e sistemas

Escreva a matriz coluna do tipo 7 x 1 tal que a i j = 2 i + 3 j .

Passo 1

Vamos interpretar o enunciado: queremos uma matriz com 7 linhas e 1 coluna, tal que o número de cada posição seja 2 * l i n h a + 3 * c o l u n a .

a 11 a 21 a 31 a 41 a 51 a 61 a 71

Passo 2

Beleza, o que queremos é isso aqui:

a 11 a 21 a 31 a 41 a 51 a 61 a 71 = 2 * 1 + 3 * 1 2 * 2 + 3 * 1 2 * 3 + 3 * 1 2 * 4 + 3 * 1 2 * 5 + 3 * 1 2 * 6 + 3 * 1 2 * 7 + 3 * 1

Fazendo as contas, encontramos a matriz que queremos:

a 11 a 21 a 31 a 41 a 51 a 61 a 71 = 5 7 9 11 13 15 17

Resposta

5 7 9 11 13 15 17

Exercício Resolvido #7

Instituto Federal Catarinense, Lista de Álgebra Linear, Marcelo Cendron, Curso de Engenharia de Controle e Automação - Adaptado

Dadas as matrizes:

A = 1 5 2 - 1 0 1 3 2 4 B = 6 1 3 - 1 1 2 4 1 3

Calcule:

a) A + B

b) - 3 A + 2 B

c) ( 3 A ) * B

Passo 1

a) Como vimos lá na teoria, pra somar matrizes basta somar elemento a elemento, assim como nos vetores. Então pra calcularmos A + B , vai ficar assim:

A + B = 1 5 2 - 1 0 1 3 2 4 + 6 1 3 - 1 1 2 4 1 3

A + B = 1 + 6 5 + 1 2 + 3 - 1 + ( - 1 ) 0 + 1 1 + 2 3 + 4 2 + 1 4 + 3

Somando os termos, chegamos em:

A + B = 7 6 5 - 2 1 3 7 3 7

Passo 2

b) Para calcularmos - 3 A + 2 B , temos que lembrar primeiramente que a multiplicação pelo escalar vem antes da soma beleza? Então primeiro vamos ter que multiplicar A por - 3 e B por 2 :

- 3 A + 2 B = - 3 1 5 2 - 1 0 1 3 2 4 + 2 6 1 3 - 1 1 2 4 1 3

Como multiplica mesmo??

Isso aí, o escalar vai multiplicar cada termo da matriz, assim:

- 3 A + 2 B = - 3 * 1 - 3 * 5 - 3 * 2 - 3 * ( - 1 ) - 3 * 0 - 3 * 1 - 3 * 3 - 3 * 2 - 3 * 4 + 2 * 6 2 * 1 2 * 3 2 * ( - 1 ) 2 * 1 2 * 2 2 * 4 2 * 1 2 * 3

Multiplicando cada termo:

- 3 A + 2 B = - 3 - 15 - 6 3 0 - 3 - 9 - 6 - 12 + 12 2 6 - 2 2 4 8 2 6

Agora é só a gente somar as matrizes, igual fizemos lá no passo 1:

- 3 A + 2 B = 9 - 1 3 0 1 2 1 - 1 - 4 - 6

Passo 3

c) Nesse caso, vamos lembrar que primeiro fazemos o que ta dentro dos parênteses, depois fazemos a multiplicação de fora. Então, multiplicando A pelo escalar 3 :

3 A * B = 3 1 5 2 - 1 0 1 3 2 4 * 6 1 3 - 1 1 2 4 1 3

3 A * B = 3 15 6 - 3 0 3 9 6 12 * 6 1 3 - 1 1 2 4 1 3

Agora sim, vamos fazer a multiplicação entre as matrizes daquele jeitinho que aprendemos na teoria:

3 A * B = 3 * 6 + 15 * - 1 + 6 * 4 3 * 1 + 15 * 1 + 6 * 1 3 * 3 + 15 * 2 + 6 * 3 - 3 * 6 + 0 * - 1 + 3 * 4 - 3 * 1 + 0 * 1 + 3 * 1 - 3 * 3 + 0 * 2 + 3 * 3 9 * 6 + 6 * - 1 + 12 * 4 9 * 1 + 6 * 1 + 12 * 1 9 * 3 + 6 * 2 + 12 * 3

Realizando a multiplicação e depois a soma dos termos, vamos ter:

3 A * B = 27 24 57 - 6 0 0 96 27 75

Resposta

a) A + B = 7 6 5 - 2 1 3 7 3 7

b) - 3 A + 2 B = 9 - 13 0 1 2 1 - 1 - 4 - 6

c) 3 A * B = 27 24 57 - 6 0 0 96 27 75

Exercício Resolvido #8

Instituto Federal Catarinense, Lista de Álgebra Linear, Marcelo Cendron, Curso de Engenharia de Controle e Automação - Adaptado

Dadas as matrizes:

A = 3 0 - 1 2 1 1 B = 4 - 1 0 2 C = 1 4 2 3 1 5

Sabendo que 1 2 C T - 1 4 A = D T e C * C T = E + B , dê as matrizes D e E .

Passo 1

Primeiro vamos calcular 1 2 C T - 1 4 A , o primeiro passo é transpor a matriz C :

1 2 C T - 1 4 A = 1 2 1 4 2 3 1 5 T - 1 4 3 0 - 1 2 1 1

1 2 C T - 1 4 A = 1 2 1 3 4 1 2 5 - 1 4 3 0 - 1 2 1 1

Agora vamos fazer a multiplicação pelos escalares:

1 2 C T - 1 4 A = 1 2 3 2 2 1 2 1 5 2 + - 3 4 0 1 4 - 2 4 - 1 4 - 1 4

Passo 2

Agora, vamos finalmente realizar a sominha dessas frações :P mas antes vamos colocar todas que vão ser somadas no mesmo denominador, assim:

1 2 C T - 1 4 A = 2 4 3 2 8 4 2 4 4 4 10 4 + - 3 4 0 1 4 - 2 4 - 1 4 - 1 4

1 2 C T - 1 4 A = 2 4 - 3 4 3 2 8 4 + 1 4 2 4 - 2 4 4 4 - 1 4 10 4 - 1 4

1 2 C T - 1 4 A = - 1 4 3 2 9 4 0 3 4 9 4 = D T

Passo 3

Ok, sabemos que esse resultado é a matriz D transposta. Então vamos transpor de novo, afinal, sabemos que D T T é a própria matriz D né?

D T T = D = - 1 4 9 4 3 4 3 2 0 9 4

É isso aí, já achamos a matriz D :)

Passo 4

Agora vamos pra C * C T = E + B , primeiro vamos transpor a matriz C igual fizemos lá no passo 1

C * C T = 1 4 2 3 1 5 * 1 3 4 1 2 5

Agora sim, bora multiplicar essas matrizes:

C * C T = 1 * 1 + 4 * 4 + 2 * 2 1 * 3 + 4 * 1 + 2 * 5 3 * 1 + 1 * 4 + 5 * 2 3 * 3 + 1 * 1 + 5 * 5

Fazendo a multiplicação e soma dos termos:

C * C T = 21 17 17 35 = E + B

Passo 5

Do enunciado, temos que

21 17 17 35 = E + B

21 17 17 35 = E + 4 - 1 0 2

Vamos passar a matriz B pro outro lado subtraindo pra encontrarmos a matriz E :

E = 21 17 17 35 - 4 - 1 0 2

E = 17 18 17 3 3

E fim :)

Resposta

D = - 1 4 9 4 3 4 3 2 0 9 4

E = 17 18 17 33

Exercícios de Livros Relacionados

36. Usando sua experiência com o exercício 35, projete um teste geral que possa ser aplicado a uma fórmula para aij para determinar se A=[a]ij é simétrica.
Se as entradas da matriz C = c 11 x c 21 x ⋮ c m 1 xc 12 x c 22 x ⋮ c m 2 x⋯ ⋯ ⋮ ⋯c 1 n x c 2 n x ⋮ c m n x São funções deriváveis de x , então definimos d C d x = c 11 ' x c 21 ' x ⋮ c m 1 ' xc 12 '
Se a b c d = m e a matriz de uma rotação em torno da origem, mostre que as colunas de m são vetores unitários ortogonais e o mesmo vale para as linhas.
Seja T:R ² →R ² ² ² a transformação linear que consiste em aplicar uma rotação de ângulo θ e depois trocar o sinal da segunda coordenada. Mostre que T é a reflexão em torno de uma reta r que contém a
Sejam r uma reta que contém a origem, α o ângulo de O X para reS :R ²→R ² ² ² a reflexão em torno de r . Sendo e 1=( 1 ,0 )ee 2=( 0 ,1 ) mostre que o ângulo de e 1 paraS e 1 é 2 α e o ângulo de e 2 pa