Escalonamento de Matrizes
Produzido por Bruno PestanaTeoria
Fala aí! Bora conversar sobre escalonamento de matrizes?
Uma matriz escalonada é uma matriz triangular superior. Ou seja, todos os elementos abaixo da diagonal principal são nulos, isso é, iguais a zero, assim:
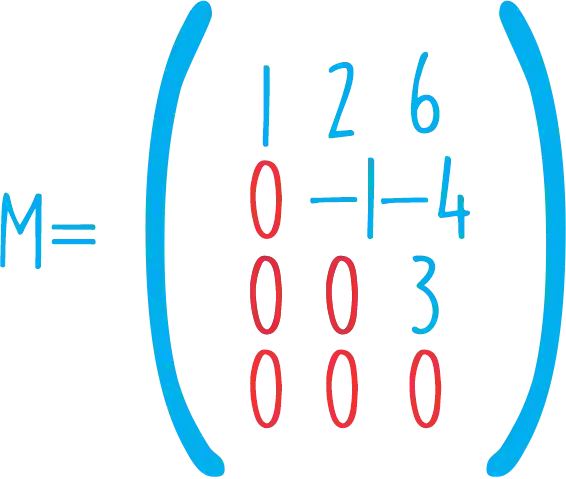
-Mas por que fazemos o escalonamento de matrizes?
Excelente pergunta! O escalonamento é um método que facilita (e muito) a resolução de sistemas lineares complexos!
O método que a gente vai aprender para escalonar matrizes é chamado de Eliminação de Gauss e para isso vamos usar as operações lineares.
Se liga nesse videozinho com tudo o que você precisa saber sobre escalonamento de matrizes 👇
Ou segue no textinho comigo! 😉
Como Escalonar uma Matriz?
Vamos aprender o passo a passo de como escalonar uma matriz na prática! 😁
Queremos escalonar a seguinte matriz:
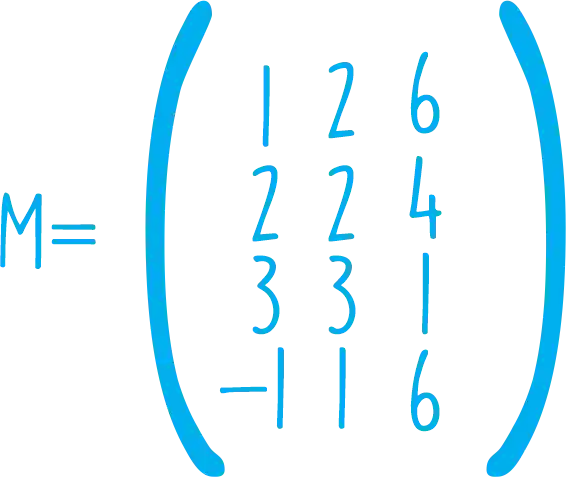
Ou seja, teremos esse processo aqui:

-Beleza, mas como a gente faz isso? Que ferramentas vamos usar!?
É o que vamos ver agora!
Regras do Jogo: Operações Lineares
Pra a gente conseguir escalonar a matriz vamos usar as operações lineares, que nada mais são do que operações feitas nas linhas da matriz que não a alteram.
Vamos usar as seguintes Operações Lineares:
- Trocar linhas de lugar:
-
;
-
- Multiplicar linhas por um escalar (diferente de zero)
-
;
-
- Trocar uma linha por uma combinação linear dela com outra linha
-
;
-
- Descartar uma linha que tenha só zeros.
Se você ainda esta desconfiado que a matriz realmente não vai mudar, eu vou te dar um exemplo que a gente usa bastante nas continhas do dia a dia!
Para isso esquece a matriz por um segundo! Vamos pensar em uma equação qualquer tipo:
Poderíamos multiplicar ou dividir o lado esquerdo e direito por um escalar qualquer e a equação continuaria igual, certo?
No nosso exemplo, vamos dividir o lado esquerdo e o direito por
Se resolvemos a equação nos dois casos, o valor de
As operações lineares seguem exatamente a mesma lógica!
Passo 1: Selecionar o Pivô da Linha 1
A ideia é zerar os elementos abaixo da diagonal principal, coluna por coluna. Então vamos começar a trabalhar os elementos da coluna
O objetivo aqui é selecionar um pivô para a linha
Para a nossa primeira linha, escolhemos o seguinte pivô:
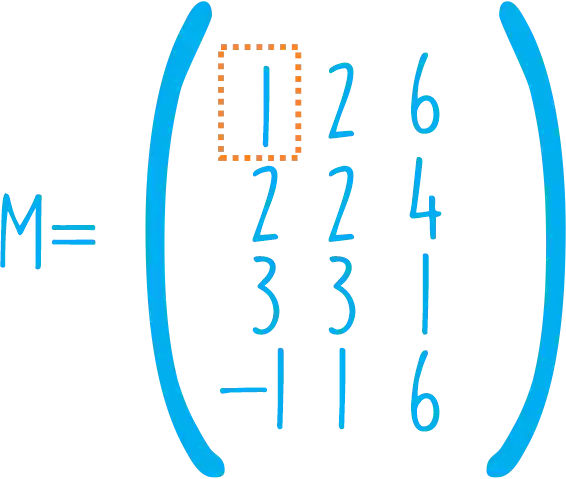
Talvez esteja meio confuso, mas confia em mim que vai ficar mais claro ao longo do processo e você vai aprender como selecionar esse pivô de uma forma esperta! 😉
Passo 2: Zerar todos os Elementos abaixo do Pivô da linha 1
Queremos zerar todos os elementos abaixo do pivô:
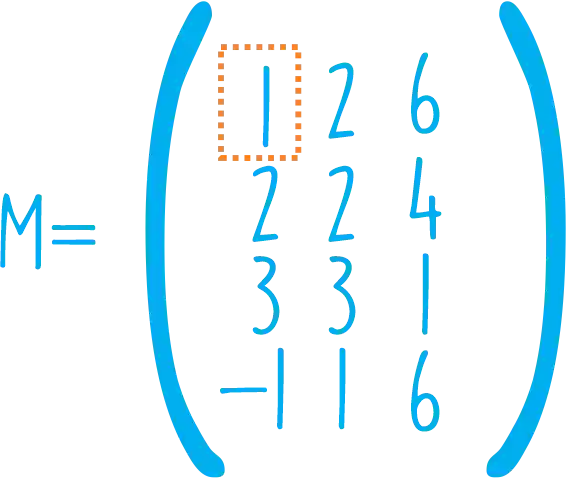
Se multiplicarmos a
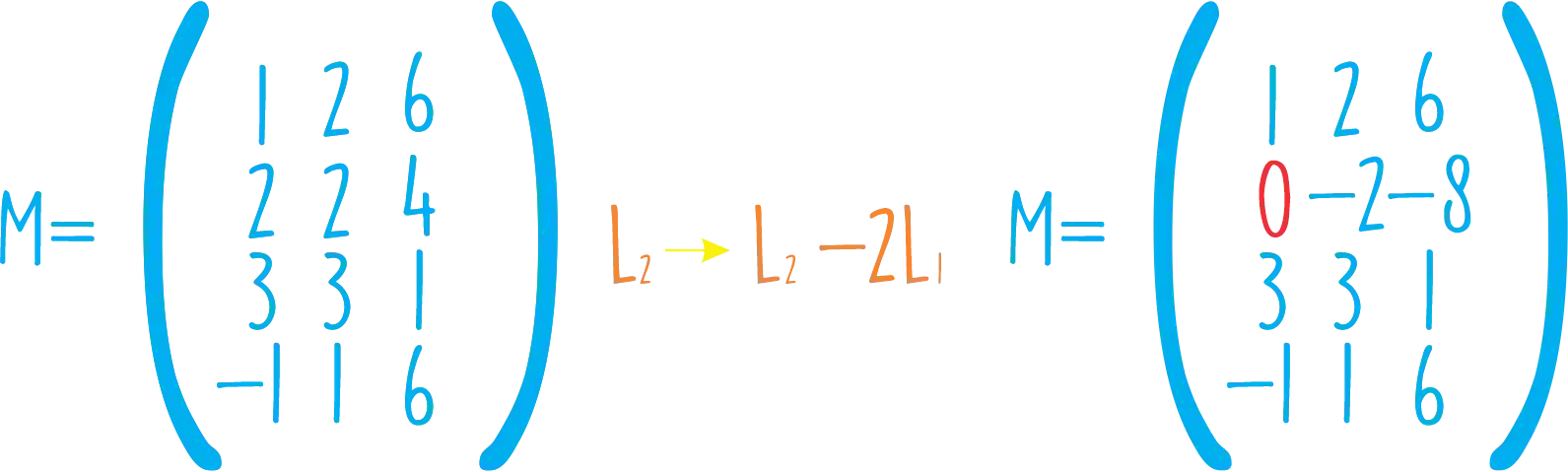
Opa! Zeramos um elemento multiplicando a linha
Agora vamos zerar o próximo elemento usando as seguintes operações lineares:
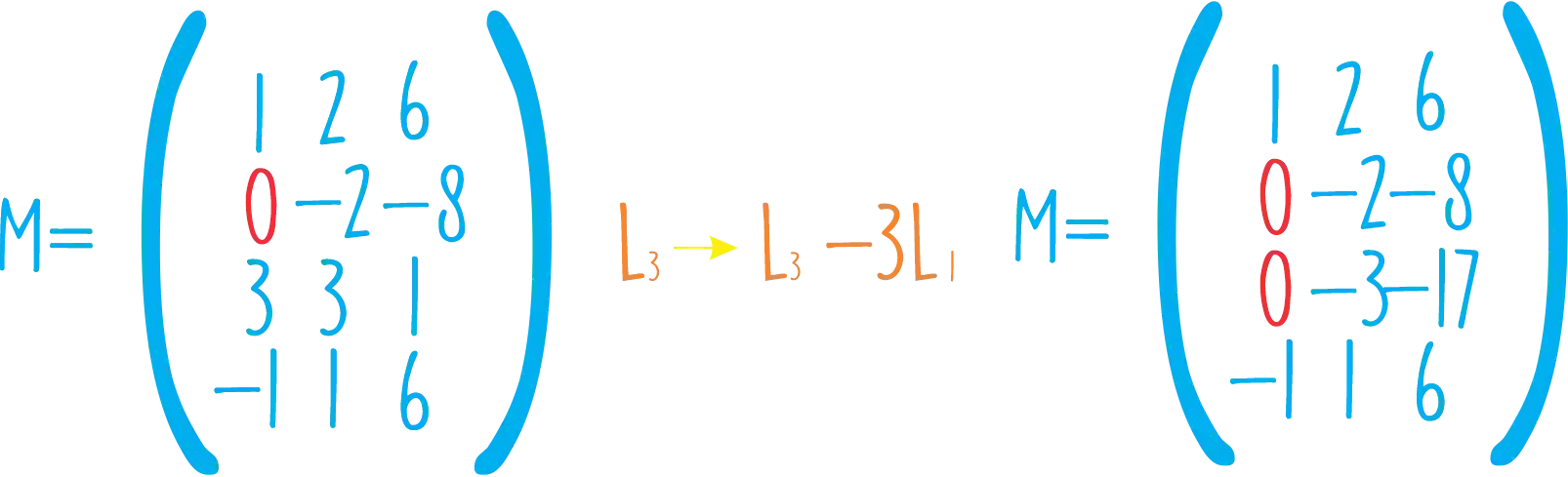
Awee! Foi outro!
Agora o último elemento:
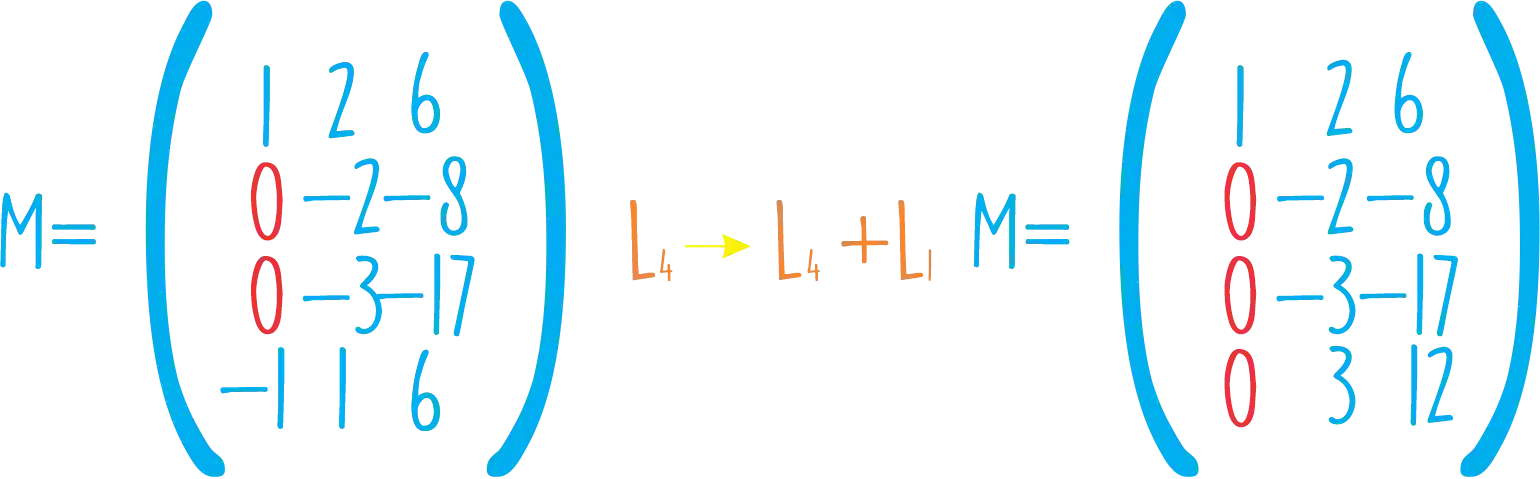
Entendeu porque o
Ele é um valor fácil de ser multiplicado por um escalar que depois irá zerar o elemento de interesse sem dificuldades! 😉
Passo 3: Selecionar o Pivô da Linha 2
Agora a nossa matriz tá com essa carinha aqui:
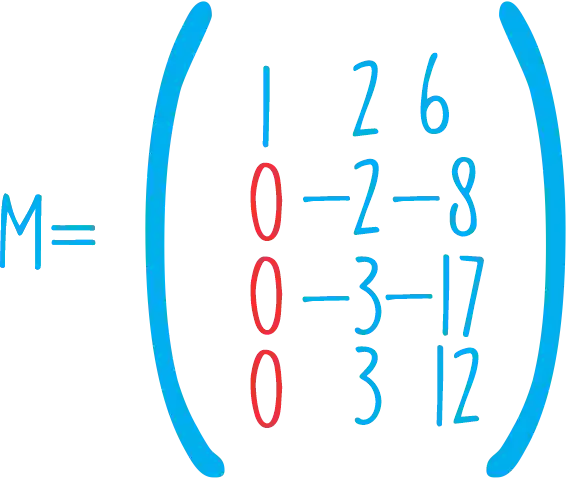
Agora, se não fizermos nenhuma operação linear, o pivô vai ser
Mas e se a gente dividir a linha
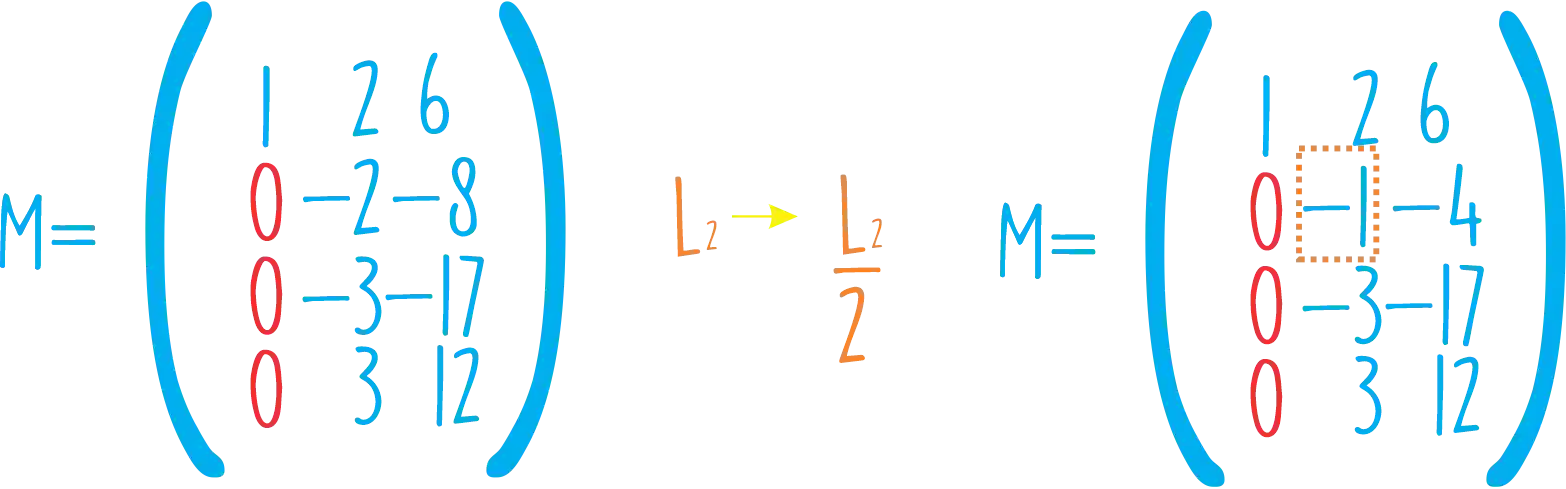
Agora o nosso pivô é o
Passo 4: Zerar todos os Elementos abaixo do Pivô da linha 2
Agora que você já entendeu o mecanismo, eu quero que você tente fazer esse passo sozinho! 😉
Depois compara com esse resultado aqui:
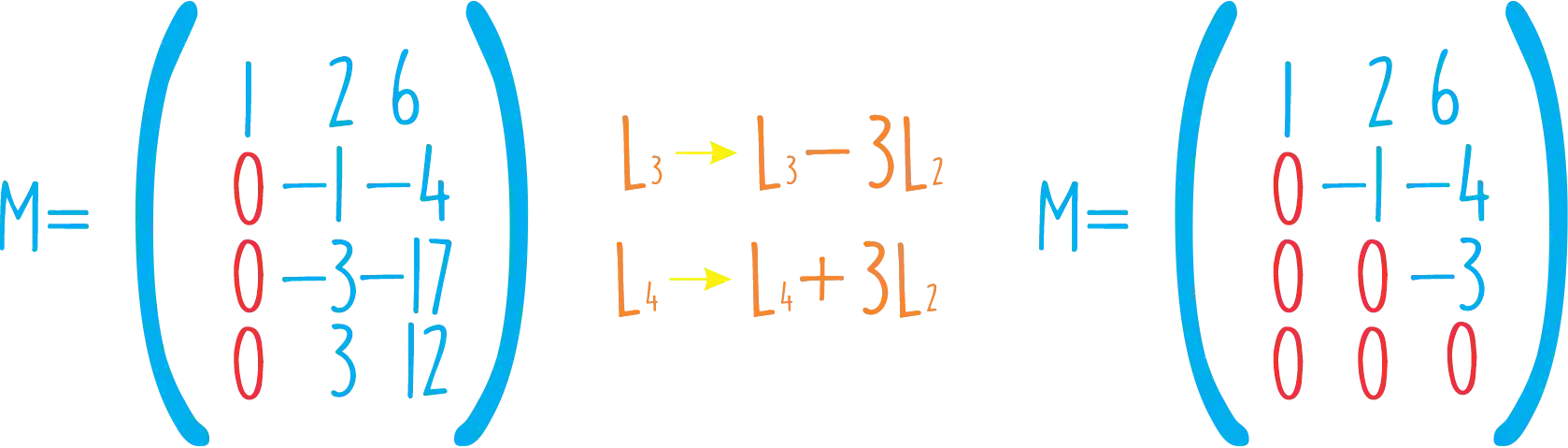
Olha que legal que aconteceu, sem querer a linha
Isso vai poupar o trabalho dos próximos passos, porque nossa matriz já esta escalonada! 😍
Se tivéssemos um valor diferente de
Passo 5: Selecionar o Pivô da Linha 3
Sem mistério! Aqui faríamos a mesma coisa dos passos
Passo 6: Zerar todos os Elementos abaixo do Pivô da linha 3
Já aqui faríamos a mesma coisa dos passos
Agora vamos praticar com exercícios?
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Escalona Aí a seguinte matriz:
Passo 1
Então, meu (minha) caro(a), sabemos que a primeira coisa a se fazer é achar o pivô da primeira linha de , tranquilo?
Show! Neste caso a gente vê que é o 1, já que é o primeiro número da primeira linha, e que é diferente de 0. Daí agora é só zerar todos os números abaixo do 1 fazendo combinações lineares. Saca só:
Daí eu faço , vou ter:
Passo 2
Agora, podemos fazer e também . E aí, teremos:
Multiplicando as linhas 2 e 3 por -1 pras coisas ficarem mais bonitas, vamos ter:
Procurando o nosso pivô, nessa vez na 2ª linha, achamos o número 1. Daí, temos que zerar tudo abaixo do 1.
Fazendo a operação , teremos...
Opa! Nem tem mais o que fazer. Nossa matriz já está escalonada, temos uma matriz triangular superior bonitinha aí. Lembrando que existem várias formas de se escalonar uma matriz, logo existem várias respostas. :D

Resposta
Exercício Resolvido #2
Elaboração Própria
Coloque a matriz abaixo em sua forma escalonada
Passo 1
ENCONTRAR O PIVÔ DA PRIMEIRA LINHA
Qual o primeiro elemento não-nulo da primeira linha?
É o !
Encontrado.
Passo 2
ZERAR A PRIMEIRA COLUNA (USANDO O PIVÔ DA PRIMEIRA LINHA)
Nesse caso só precisamos zerar o logo abaixo do pivô, pois os outros elementos já são zero.
Fazendo :
Passo 3
ENCONTRAR O PIVÔ DA SEGUNDA LINHA
O primeiro elemento não nulo da segunda linha é o .

Esse é o momento de dar um stop no que você tá fazendo para ver se tem como transformar o pivô em !
Fazendo:
A nossa matriz fica:
Passo 4
ZERAR A SEGUNDA LINHA
Agora que o nosso pivô já é , é só fazermos
Aí a matriz fica:
Já está em sua forma escalonada, mas vamos nos acostumar sempre a descartar as linhas nulas:
Resposta
Exercício Resolvido #3
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 60 – Prob. 2.4
Determine a forma totalmente escalonada das matrizes abaixo:
Passo 1
Letra
Podemos ver que nosso pivô é igual a , então vamos zerar todo mundo abaixo dele:
Agora vamos olhar pra segunda linha. O pivô dela é o , logo vamos zerar todo mundo em baixo dele:
Antes de continuar vamos já ajeitar esse nosso pivô ai da segunda linha, e transformá-lo em :
Agora, só zerar os elementos acima do pivô da segunda linha:
Pronto é isso aí.
Passo 2
Letra
Só fazer a mesma coisa da letra anterior.
Agora vamos dar uma ajeitada nos pivôs:
Passo 3
Agora vamos zerar as entradas acima dos pivôs:
Ufa!
Resposta
Exercício Resolvido #4
UFRJ-P1-2016.1
A partir de uma matriz e através da seguinte sequência de operações elementares:
;
;
;
,
Obtém-se a matriz .
Qual dentre as seguintes é a matriz ?
Obs.: Na notação utilizada, indica que a -ésima é substituída por ela mesma acrescida de vezes a -ésima linha e indica a troca das linhas e .
Passo 1
Bom, tudo o que precisamos fazer aqui é seguir a operação inversa de tudo o que foi feito com a matriz né! Se liga:
Resposta
Letra
Exercício Resolvido #5
USP, Aula de sistemas lineares - Adaptado
Encontre uma matriz escalonada equivalente à seguinte matriz:
Passo 1
Vamos por partes. O primeiro pivô não nulo da primeira linha é o . Temos que zerar tudo que estiver embaixo dele, no caso só falta o da terceira linha né?
Pra zerar esse , podemos fazer , vai ficar assim:
Passo 2
Agora bora achar o primeiro pivô não nulo da segunda linha. É o certo??
Precisamos zerar esse da terceira linha, afinal, o objetivo é zerar tudo que estiver embaixo do pivô ;) Pra facilitar nossa vida, vamos transformar o pivô em e o em também beleza? Pra isso vamos fazer as operações:
Isso vai nos dar:
Passo 3
Agora que o pivô da segunda linha é e embaixo dele também temos um , as coisas ficam mais fácil pra zerarmos o , vamos fazer a operação :
Prontinhoo, matriz escalonada :D
Resposta
Exercício Resolvido #6
USP, Aula de sistemas lineares - Adaptado
Dada a matriz
Dê sua forma escalonada.
Passo 1
Antes de tudo, acho que pra todos nós é mais complicadinho trabalhar com números decimais né? Então pra facilitar nossa vida, vamos multiplicar todas as linhas por :
Agora vamos dividir a primeira linha por , pois todos os elementos dela são múltiplos de :
Agora sim, podemos começar hehe
Passo 2
O primeiro pivô não nulo da primeira linha é . Vamos zerar todos os elementos abaixo dele.
Pra zerarmos o , podemos fazer . Eu não tirei isso da cartola, é porque vamos pensar no seguinte: queremos sumir com o , pra isso, devemos subtrair ele mesmo. Mas nenhuma linha tem outro , então o que a gente faz? Uma um múltiplo comum e multiplica cada linha por ele. Por exemplo, no caso, um múltiplo comum de e é . Então multiplicamos a primeira linha por e a segunda por para termos o mesmo número e podermos sumir com o que está embaixo do pivô
Voltando, vamos fazer então o :
Passo 3
Agora temos que sumir com o da terceira linha. Vamos fazer analogamente ao passo 2: um múltiplo comum entre e é , então multiplicamos a primeira linha por e a terceira por , então vamos fazer a operação
Passo 4
Agora vamos encontrar o primeiro pivô não nulo da segunda linha. É o certo? Então vamos sumir com o embaixo dele. Pra isso vamos fazer
Repara que essa matriz ta meio diferente das escalonadas normalmente. Mas ela ta escalonada sim viu? Mais pra frente vamos ver o que significa esse escalonamento esquisitão hehe
Resposta
Exercício Resolvido #7
Elaboração própria
Dada a matriz
Sabendo que sua forma escalonada é, quais são os valores de , e ?
Passo 1
Vamos escalonar a matriz então. O primeiro pivô não nulo da primeira linha é o certo? Então vamos zerar tudo que estiver embaixo dele, começando pelo da segunda linha.
Pra zerarmos o , podemos fazer , afinal, , vamos ficar com isso:
Agora vamos zerar esse da terceira linha, podemos fazer :
Passo 2
Agora vamos encontrar o primeiro pivô não nulo da segunda linha. É o certo? Vamos zerar o que ta embaixo dele, pra isso vamos fazer :
Opa, essa matriz escalonada é diferentona hehe a gente vai ver mais sobre essa situação lá em sistemas lineares.
Mass, de qualquer forma, encontramos os valores de , e , que são:
Resposta
Exercício Resolvido #8
Elaboração própria
Considere as afirmativas abaixo:
I – A matriz não pode ser escalonada, pois não é uma matriz quadrada.
II – Se escalonarmos completamente a matriz , vamos ter como resultado uma matriz identidade de ordem 4
III – Para escalonar uma matriz, temos que encontrar os pivôs e ir realizando operações entre as linhas até encontrarmos uma matriz triangular inferior.
Estão corretas apenas:
a) I
b) II
c) III
d) I e III
e) I e II
f) II e III
Passo 1
Vamos lá analisar cada uma das afirmativas:
I – Falsa. Não são só as matrizes quadradas que podem ser escalonadas viu galera?
II – Bora escalonar essa matrizona hehe
Para escalonar completamente, vamos dividir as linhas 2, 3 e 4 por :
Opaa, chegamos numa matriz identidade de ordem 4, então essa afirmativa é verdadeira :)
III – Falsa. Queremos chegar em uma matriz triangular SUPERIOR hehe
Como só a afirmativa II é verdadeira, a alternativa correta é a letra b!!
Resposta
b) II