Complemento Ortogonal
Teoria
Que diabos é isso? É bem intuitivo na verdade:
Vamos pegar um conjunto qualquer. O Complemento Ortogonal de seria um outro conjunto , cujos elementos são ortogonais aos elementos de . Sempre um conjunto em relação ao outro!
Por exemplo, no : vamos pensar em sendo um plano horizontal. Qual seria o conjunto , cujos elementos são todos ortogonais a ???? Uma reta vertical! Olhe o desenho abaixo:
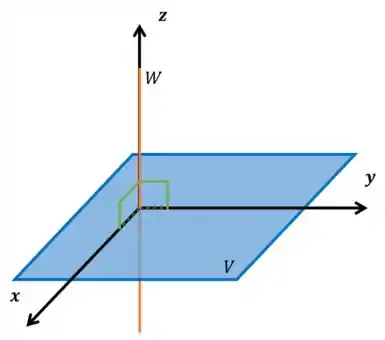
Agora que já entenderam vamos dar uma olhada na definição formal que seu professor vai passar pra vocês haha.
Notação: Simbolizamos o complemento ortogonal de , como (lê-se perp)
E lá vai um bizu: sempre, sempre mesmo, será um subespaço vetorial!
Calculando o Complemento Ortogonal
Tá, mas como eu acho quem é o complemento ortogonal de um outro conjunto? Vamos aprender vendo um exemplo:
Sendo , ache .
Eu sei que se eu pegar um vetor qualquer de e um vetor qualquer de e fizer o produto interno entre eles, tem que dar zero. Então, vou chamar de um vetor genérico do , fazer o produto interno dele com os vetores que eu tenho de e igualar a zero.
Agora fazendo o produto interno vemos que chegamos em um sistema linear homogêneo:
Posso representá-lo assim também:
Agora é só resolver isso aí.
Mas pera, vamos analisar o que estamos fazendo, estamos achando a solução do sistema linear homogêneo ou núcleo da matriz em que as linhas são os vetores da base de
Então sempre que quisermos achar o complemento ortogonal de um espaço , pegamos os vetores da base de , jogamos nas linhas de uma matriz, e encontramos seu núcleo.
Agora sim:
Logo, temos que:
Nosso vetor genérico de é dado por
Portanto:
Calculando o Complemento Ortogonal
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Sabendo que , represente como um espaço gerado.
Passo 1
Temos que achar um conjunto de vetores que sejam ortogonais aos vetores de . Vamos jogar os vetores geradores de nas linhas de uma matriz :
Agora, encontramos o núcleo dela:
Que moleza, a matriz já está até escalonada haha. Temos então que:
Passo 2
Podemos ver que o nosso vetor genérico é:
E assim:
Resposta
Exercício Resolvido #2
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 162 – Prob 5.3
Determine uma base de , onde
é a reta em dada por
é o plano em dado por
Passo 1
Pela equação da reta temos que . Logo:
O vetor genérico de tem a forma:
Então, para acharmos uma base para , basta acharmos o vetor ortogonal à :
O vetor genérico de é dado por:
Portanto,
Outra forma possível era termos pensado que, como estamos no , o complemento ortogonal de uma reta será sempre a reta perpendicular a ela.
Sendo assim, podemos obter o vetor gerador de simplesmente pegando os coeficientes da equação que nos foi dada:
Passo 2
Dessa vez vamos usar a cabeça haha. Temos um plano no . Portanto, seu complemento ortogonal será a reta perpendicular a ele concorda? Podemos obtê-la simplesmente pegando os coeficientes da equação do plano:
Passo 3
Agora não tem jeito, vamos jogar os geradores de nas linhas de uma matriz e calcular seu núcleo:
Temos então que:
O vetor genérico de é dado por:
Logo:
Passo 4
Novamente, jogamos os vetores geradores nas linhas de uma matriz, e calculamos seu núcleo:
Tomando como vetor genérico do , temos:
Então, o vetor genérico de tem essa cara:
Portanto,
Resposta
Exercício Resolvido #3
Elaboração própria
Foi pedido a Carolzinha que provasse a proposição:
“Se são ortogonais a , então , sendo é base de ”
Assim Carolzinha deu a seguinte resposta:
“Devemos primeiramente construir a base de . E assim, é uma possível base de . Assim, vamos fazer o seguinte:
Usando as propriedades do produto interno:
E assim, aplicando a hipótese, vamos ter em todos os casos . E assim, como , é verdade que ”
Sabendo que Carolzinha está errada, qual foi o erro de Carolzinha?
Passo 1
Carolzinha fez o produto interno de , que queríamos saber se pertencia à , com os vetores da base de e igualou a zero. Isso quer dizer que ela achou que o complemento ortogonal é formado por vetores ortogonais, e isso não é necessariamente verdade.
O complemento ortogonal não é um conjunto ortogonal, ele é ortogonal aos vetores de .
Passo 2
O que Carolzinha deveria ter feito era ter utilizado o fato de que, se são ortogonais a , então:
Assim basta somar :
Passo 3
Reorganizando:
E assim, vemos que é exatamente o complemento ortogonal.
Resposta
Ei, a resposta está no passo a passo :)