Exercícios Resolvidos de Ângulo de Torção e Problemas Estaticamente Indeterminados
Ver TeoriaEnunciado
O eixo de aço A-36 tem diâmetro de e está preso nas extremidades e . Se for submetido ao momento, determine a tensão de cisalhamento máxima nas regiões e do eixo.
Dados: .
Passo 1
O que está acontecendo?
O eixo tem um módulo de elasticidade transversal , um diâmetro e, consequentemente, um raio .
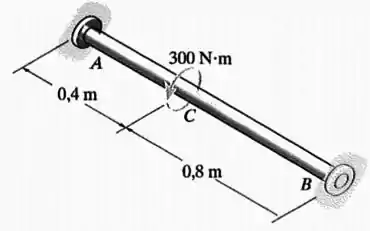
Ele está submetido a um torque no ponto .
E ele está preso nas extremidades e , que realizam torques de reação nele de forma a manter o seu equilíbrio.
Usando a regra da mão direita, obtemos o seguinte DCL (diagrama de corpo livre) para esse eixo:
Aplicando as condições de equilíbrio nesse eixo, vamos ter uma única equação (equilíbrio de torques), mas duas incógnitas ( e ).
Isso significa que esse é um problema estaticamente indeterminado.
Então também vamos precisar de uma equação de compatibilidade para resolver o exercício.
Qual vai ser a equação de compatibilidade nesse caso?
Nesse caso, temos que o eixo está fixo nos pontos e .
Assim, temos que o ângulo de torção entre esses dois pontos deve ser igual à zero:
Mas o ângulo de torção entre esses dois pontos é igual à soma dos ângulos de torção do trecho e do trecho :
Essa vai ser a nossa equação de compatibilidade.
Para que ela seja útil, vamos precisar descrever os ângulos de torção de cada trecho do eixo usando a fórmula:
E o que é que o exercício quer?
Ele quer saber a tensão de cisalhamento máxima nas regiões e do eixo.
Essas tensões máximas podem ser calculadas usando a fórmula da torção:
Mas... para poder usar essas fórmulas, precisamos antes conhecer os torques internos nos trechos e desse eixo.
E para conhecer esses torques, vamos ter que usar o equilíbrio de torques e a equação de compatibilidade acima.
Passo 2
Então vamos começar o exercício identificando os torques internos nos trechos e do eixo.
Começamos pelo DCL do eixo:
Em seguida, fazemos uma análise dos esforços internos: secionamos o eixo em cada trecho e observamos os esforços internos nessas seções.
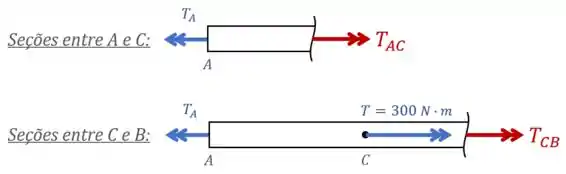
Nessa análise, desenhamos os torques internos em vermelho “saindo” da peça pois essa é a nossa convenção.
Caso os seus professores utilizem a convenção contrária (a de que os torques internos são positivos quando “entram” nas peças), você deve desenhar os torques internos entrando.
Aplicando o equilíbrio de torques em cada caso, temos que:
Isolando os torques e , encontramos que:
Passo 3
Agora que já definimos os torques internos e nos diferentes trechos do nosso eixo, podemos estudar a nossa equação de compatibilidade:
Aplicando a fórmula do ângulo de torção para cada trecho, e tendo em mente que os dois trechos possuem:
- O mesmo módulo de elasticidade transversal ;
- E a mesma seção transversal circular maciça de raio , e, consequentemente, o mesmo momento de inércia polar ,
Essa equação fica assim:
Multiplicando tudo por , temos que:
Substituindo e :
E fazendo as multiplicações, temos que:
Colocando em evidência, isso fica assim:
E, finalmente, isolando , encontramos que:
Substituindo e , isso nos diz que:
Assim, temos que os torques internos e no nosso eixo são:
Passo 4
Por fim, agora que já conhecemos os torques e resistido por cada trecho do eixo, podemos calcular as tensões de cisalhamento máxima em cada trecho.
Para tanto, usamos a fórmula da torção:
Para ambos os trechos do eixo, que são ambos maciços e de raio , o momento polar de inércia vai ser igual à .
Dessa forma, temos que:
Simplificando, isso fica assim:
Aplicando essa expressão para o trecho , temos:
Substituindo , temos:
Finalmente, substituindo os valores:
- ;
- & ,
- ;
- & ,
Encontramos que:
Agora, como , isso significa que:
Fazendo o mesmo procedimento para , temos:
Substituindo , temos:
Por fim, substituindo os valores:
Encontramos que:
Como para a nossa resposta, só importa a intensidade da tensão de cisalhamento máxima , retiramos o sinal de negativo na hora de fornecer a nossa resposta final:
E assim finalizamos o exercício!