Erro na Interpolação
Produzido por Bruno PestanaTeoria
Introdução Erro Exato
Fala meus amigos, tudo certinho? Veja bem, quando nós estudamos anteriormente os polinômios interpoladores nós vimos que são aproximações de uma função real, e essas aproximações podem ser tãaaaaaaao próximas quanto nós quisermos. O lance é, como toda aproximação, nossa função terá um erro (tava demorando né?).
Então, vamos dar uma estudada nesse erro da interpolação! Vamos aprender um negócio que basicamente é apresentar um limitante pro erro envolvido na aproximação de uma função feita por um polinômio interpolador.
Imagina a seguinte situação:
Seja . Usando a tabela abaixo encontre um polinômio interpolador de grau e calcule:
![]()
(a) uma aproximação para
(b) o erro desta aproximação
(c) um limitante para o erro
(d) uma aproximação para o erro assumindo que não é conhecida.
Usaremos esse exemplo para explicar a teoria, vem comigo!
Primeiro o item (a).
O exercício está pedindo uma aproximação para . Já aprendemos vários métodos para calcular uma aproximação e podemos usar qualquer um deles porém, como em seguida o exercício pede o erro, faça pelo método de Newton (a menos que o enunciado mande você fazer por outro método, é claro). Isso porque para calcular a aproximação do erro precisamos da tabela de diferenças divididas! Então já que vamos ter que montá-la de qualquer jeito, aproveitamos e já fazemos a aproximação pelo método de Newton.
Uma dica: se você quer estimar o erro em um polinômio de grau , calcule os operadores até grau já que vamos precisamos do maior operador diferenças divididas de ordem ! (não se preocupe logo fará sentido!). Nesse caso, o polinômio que o exercício quer é de grau então vamos fazer a tabela até ,
Passo 1. Vamos montar nossa tabela! Ela fica assim:
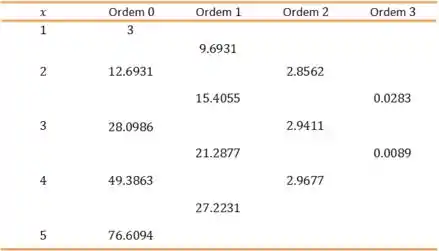
Repare que com nós poderíamos ter calculado até a Ordem , mas como não vamos precisar dela melhor evitarmos trabalho haha.
Passo 2. Como queremos uma aproximação para , vamos usar , e . Da tabela, temos:
Nosso polinômio de grau é:
Passo 3. Nossa aproximação será:
Erro Exato
Para resolver o item (b), precisamos saber o que é o erro exato.
Como já falamos anteriormente, sempre que realizamos uma aproximação não obtemos o valor verdadeiro da função certo? (justamente por se tratar de uma aproximação). Existe um erro entre o polinômio e a função, e a diferença entre os dois nós chamamos de Erro Exato.
Tendo uma função e sua função interpoladora , calculamos o erro como:
Pronto! já sabemos responder o item (b) do nosso exemplo:
O erro exato é:
Limitante para o erro
O item (c) pede uma limitante para o erro. Ou seja, ele quer saber o erro máximo que seu polinômio interpolador vai ter naquele intervalo que você está aproximando . E como fazemos isso?
Seja uma função definida e (n+1) vezes diferenciável num intervalo [a,b]. Nós temos os pontos , , ..., , (n+1), que são pontos igualmente espaçados.
Ou seja, se deste intervalo. Se interpola nestes pontos, então o limitante superior para o erro é dado:
E o o valor máximo do módulo das derivadas de ordem de no intervalo , ou seja, o maior valor em módulo das derivadas da função aplicadas no intervalo
Mas, o que são pontos não serem equidistantes? Então:
Vamos tentar resolver o item (c) agora?
Para encontrarmos um limitante para o erro precisamos da derivada terceira de para calcular o valor Máximo :
Como essa função é contínua, decrescente e positiva no intervalo , ela terá seu maior valor em módulo em , onde:
Como os valores de são igualmente espaçados de :
Repare que usando essa forma, o resultado independe do valor , ou seja, obtemos o valor máximo do erro no intervalo .
Estimativa para o erro
No último item do nosso exemplo pede uma aproximação para o erro assumindo que não é conhecida. Veja bem, o problema vem agora. Geralmente não conhecemos nossa (daí a necessidade de encontrarmos uma aproximação), e o nosso nunca é conhecido, na maioria dos casos não podemos calcular o erro e nem um limitante para ele! Além disso, nem sempre a aproximação baseada em todos os pontos é a que se aproxima mais do valor verdadeiro.
Lembra que lá no começo, na hora de calcular a aproximação pelo método de Newton, eu falei para calcularmos ? Uma ordem acima da necessária para o polinômio? Então agora que ele entra em cena.
Bom, por sorte algum maluco percebeu que:
Onde são os operadores diferenças divididas de ordem ! Nesse caso, dizemos que:
Voltando agora para o nosso exemplo:
Imaginamos que não conhecemos a e vamos calcular uma aproximação para o erro. O maior operador diferenças divididas de ordem é:
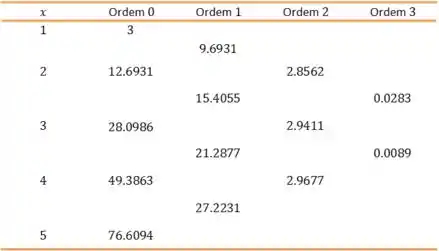
Aplicando agora a fórmula:
Que é uma aproximação razoável para .
Pronto galera! Concluímos o exemplo. Partiu botar em prática agora!
Erro Exato
Limitante para o erro
Estimativa para o erro
Exercícios Resolvidos
Exercício Resolvido #1
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 256, exercício 2
Verifique que na interpolação linear
onde .
Passo 1
Como na interpolação linear nós só temos dois pontos, sempre podemos dizer que os pontos são igualmente espaçados haha. Logo, sempre é válida a fórmula:
Substituindo já que estamos usando interpolação linear,
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 257, exercício 5
Queremos construir uma tabela que contenha valores de para pontos igualmente espaçados no intervalo .
Qual deve ser o menor número de pontos desta tabela para se obter, a partir dela, o , usando interpolação linear com erro menor que para qualquer no intervalo .
Passo 1
Nesse caso usaremos o número de pontos como uma forma de “dimensionar o ”. Em uma interpolação linear temos apenas dois pontos separados por uma distância . Logo, sempre podemos dizer que:
Vamos começar encontrando . Precisamos da derivada segunda de :
Como o erro deve ser menor que no intervalo , usamos o valor máximo de nesse intervalo como . E esse valor é em , onde .
Passo 2
Agora precisamos escrever em função do número de pontos. Então vamos montar uma tabelinha:

Com essa relação podemos substituir tudo na fórmula:
Resolvendo a equação de segundo grau, temos:
Como não faz sentido termos um número de pontos negativo e nem quebrado, pontos.
Resposta
Exercício Resolvido #3
Lista 4 – Professor Mauro – UFRJ – Questão 5
Deseja-se construir uma tabela da função no intervalo com pontos igualmente espaçados. Seja o passo. Qual o valor máximo de para que o erro da interpolação linear em qualquer ponto do intervalo seja menor ou igual a .
Passo 1
Em uma interpolação linear temos apenas dois pontos separados por uma distância . Logo, sempre podemos dizer que:
Vamos começar encontrando . A derivada segunda de é ela mesma. Também sabemos que é crescente e positiva em , logo tem seu maior valor em , onde .
Passo 2
Agora basta substituirmos tudo na fórmula:
Como a diferença entre os pontos é medida em módulo, .
Resposta
Exercício Resolvido #4
Lista 4 – Professora Angela – UFRJ – Questão 5
Seja a função , calcule uma aproximação para , utilizando o polinômio de Newton sabendo que ; ; . Dar um limitante superior para o erro.
Passo 1
Vamos começar montando a tabela de operadores diferenças divididas:

Como temos apenas pontos, vamos encontrar um polinômio interpolador de grau .
Passo 2
Definimos , e e tiramos da tabela que:
Substituindo no polinômio temos:
Passo 3
Nossa aproximação será:
Passo 4
Como os pontos estão igualmente espaçados, um limitante superior para o erro pode ser dado por:
Temos que e . Só falta acharmos . Para isso, precisamos da derivada terceira de :
Como queremos o maior módulo de em , basta acharmos o máximo de . Como é decrescente e positiva em , seu máximo está em , onde temos .
Substituindo tudo na nossa equação:
Resposta
Exercício Resolvido #5
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 257, exercício 7
Sabendo-se que a equação admite uma raiz no intervalo , determine o valor desta raiz usando interpolação quadrática. Estime o erro cometido, se possível.
Passo 1
Vamos começar montando uma tabela com alguns pontos:
![]()
O que vamos fazer agora é escrever como função de e não mais como função de . Ficamos com:
![]()
Assim nós não precisamos encontrar o zero do polinômio interpolador. Podemos jogar o zero direto no que vamos encontrar! Agora é só seguirmos o passo a passo de sempre ;)
Como ele quer uma função de interpolação quadrática, precisamos de pontos. Vamos usar , e . Além disso para estimarmos a incerteza precisamos de um quarto ponto para obtermos um operador diferenças divididas de ordem . Vamos usar então o . A tabela fica:
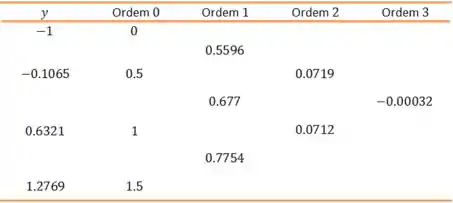
Passo 2
Da tabela tiramos que:
Substituindo no polinômio:
Substituindo ,
Passo 3
Agora para estimar o erro usamos a fórmula:
Resposta
Exercício Resolvido #6
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 257, exercício 6
Consideremos o problema de interpolação para , numa tabela de pontos igualmente espaçados com intervalo , usando um polinômio de grau. Fazendo , , mostre que:
Passo 1
Temos que:
Como estamos usando um polinômio interpolador de segundo grau, temos , e precisamos da derivada terceira de :
E temos que o valor máximo que assume em é . Sendo assim, substituindo e os valores de e dados:
Passo 2
Não é isso que queríamos né? Po, mas se é sempre menor que , então se acharmos o máximo do polinômio , então teremos um máximo geral para o erro! Vamos tentar isso!
O máximo de certamente é um ponto crítico de , então:
Substituindo esses valores na função:
Logo,
Substituindo, temos:
Aê, agora sim! Esse era o valor que precisávamos!
Passo 3
Repare que aquela informação dos pontos serem igualmente espaçados era só pra te enganar mesmo haha! Se usasse a fórmula você ia chegar em:
que não é o resultado que ele quer haha.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Lista 6 – Professora Susana – Questão 3
Suponha que é aproximada em por um polinômio interpolador em pontos distintos equidistantes . Determine tal que o erro seja menor que
Passo 1
Como temos pontos equidistantes podemos usar a fórmula:
Temos muitas incógnitas aí né? Vamos diminuir isso um pouco. Primeiro escrevemos em função de . Lembrando que aqui é o número de partes em que o intervalo foi dividido e não o número de pontos!

Passo 2
Agora vamos dar um jeito nesse .
Bom, se for ímpar, a derivada de ordem de seno será um seno. O sinal do seno não importa já que estamos interessados no módulo dele. Nesse caso, que é o valor de .
Se for par, a derivada de ordem de seno será um cosseno. Nesse caso, que é o valor de .
Então para cuidar desses dois casos vamos usar a variável :
Vamos substituir ambos os casos na nossa fórmula e achar o mínimo que satisfaz a equação.
Passo 3
Caso par:
Se , temos:
Se , temos:
Logo, .
Passo 4
Caso ímpar:
Se , temos:
Se , temos:
Se , temos:
Logo,
Passo 5
Sendo assim, o menor é .
Resposta