Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Interpolação de Newton

Ver Todos os Exercícios

Teoria

A Interpolação de Newton, também chamada de forma de Newton é mais um jeito de se aproximar uma função, achando seu polinômio interpolador.

Ilustração de Isacc Newton
Ilustração de Isacc Newton

O objetivo é aproximar uma função para um polinômio . Vamos utilizar esse método sempre que tivermos pares ordenados da função, mas ou menos assim:

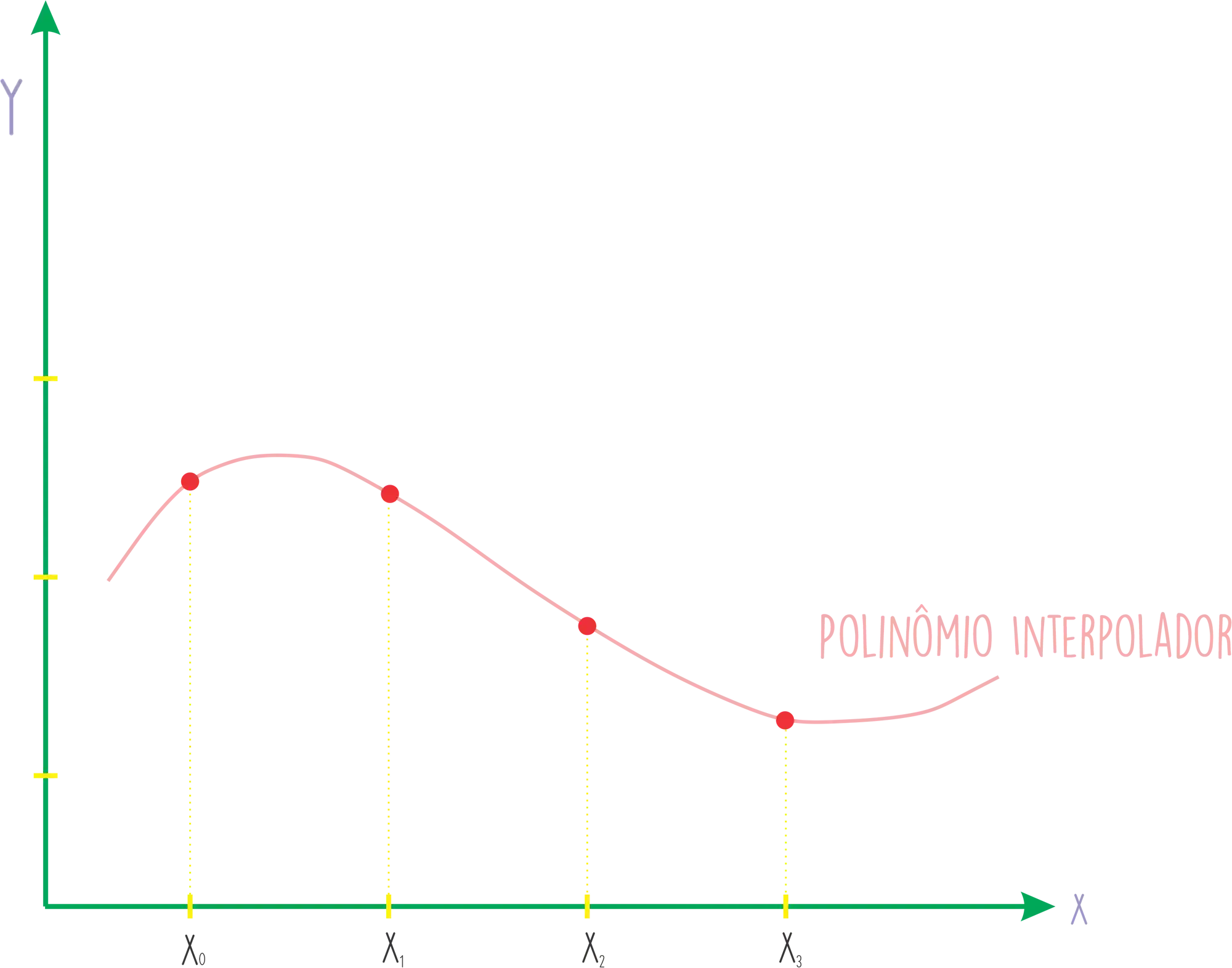
Interpolação de Newton
Interpolação de Newton

Esses pontinhos em vermelho no gráfico são os pontos que a gente conhece. Com o método de Newton a gente consegue traçar um polinômio interpolador… ou seja, um polinômio que passa por esses pontos! 🤩

Fórmula do polinômio interpolador de Newton

Indo direto ao ponto, a fórmula do polinômio interpolador por Newton é dada por :

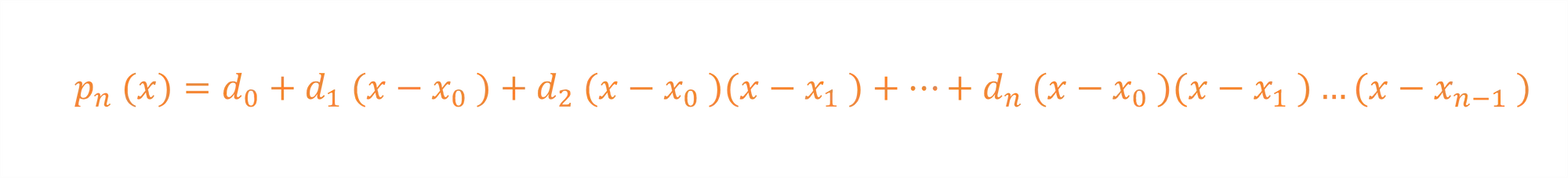
Polinômio interpolador de newton
Polinômio interpolador de newton

Onde:

  • são chamados de operadores diferenças divididas;
  • são os extremos dos intervalos que dividimos a função (o dos pontos que temos).

Ok, mas o que são esses operadores diferenças divididas? Bora descobrir?!

📢 Clique para ver mais:

Como achar o grau do polinômio interpolador: Operador diferenças divididas

Para achar o polinômio interpolador de Newton, vamos precisar de um operador chamado de diferenças divididas que são os polinômio interpolador :

Se quisermos calcular o valor de no polinômio teremos:

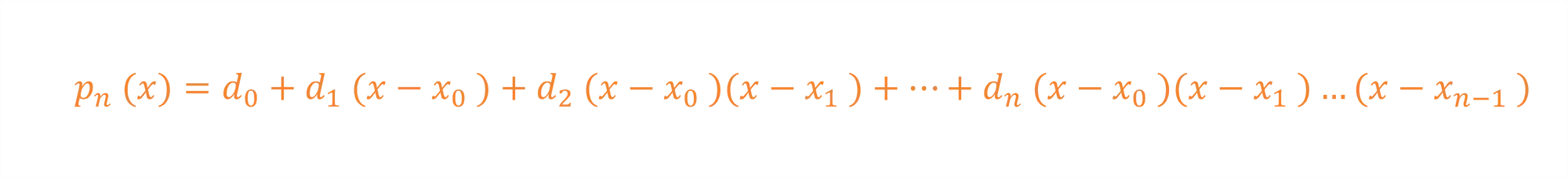
Polinômio interpolador de newton
Polinômio interpolador de newton

Note que todos os termos que possuem vão se cancelar e irá restar apenas:

Agora vamos tentar calcular através de :

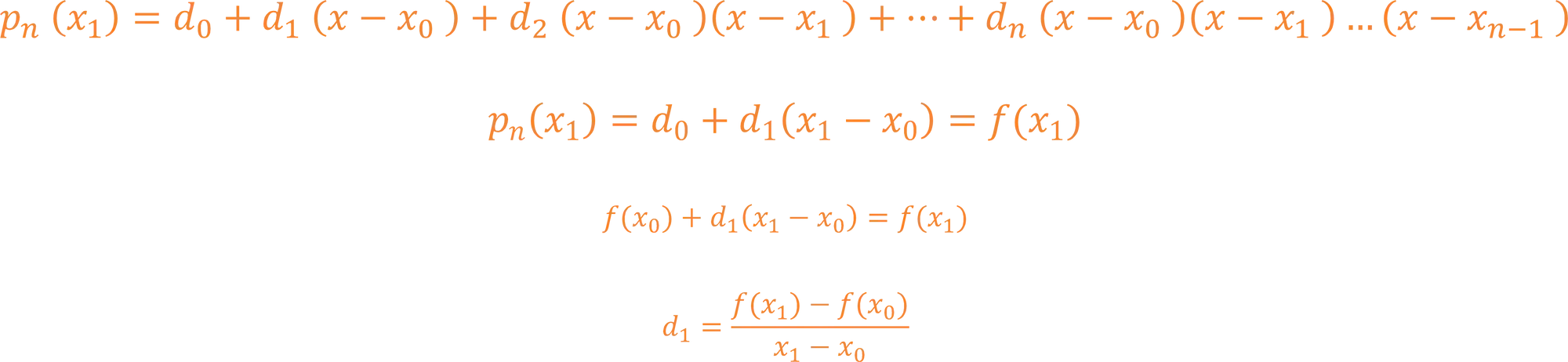
Interpolação de Newton: Cálculo de d1
Interpolação de Newton: Cálculo de d1

Podemos colocar esse resultado em uma tabelinha:

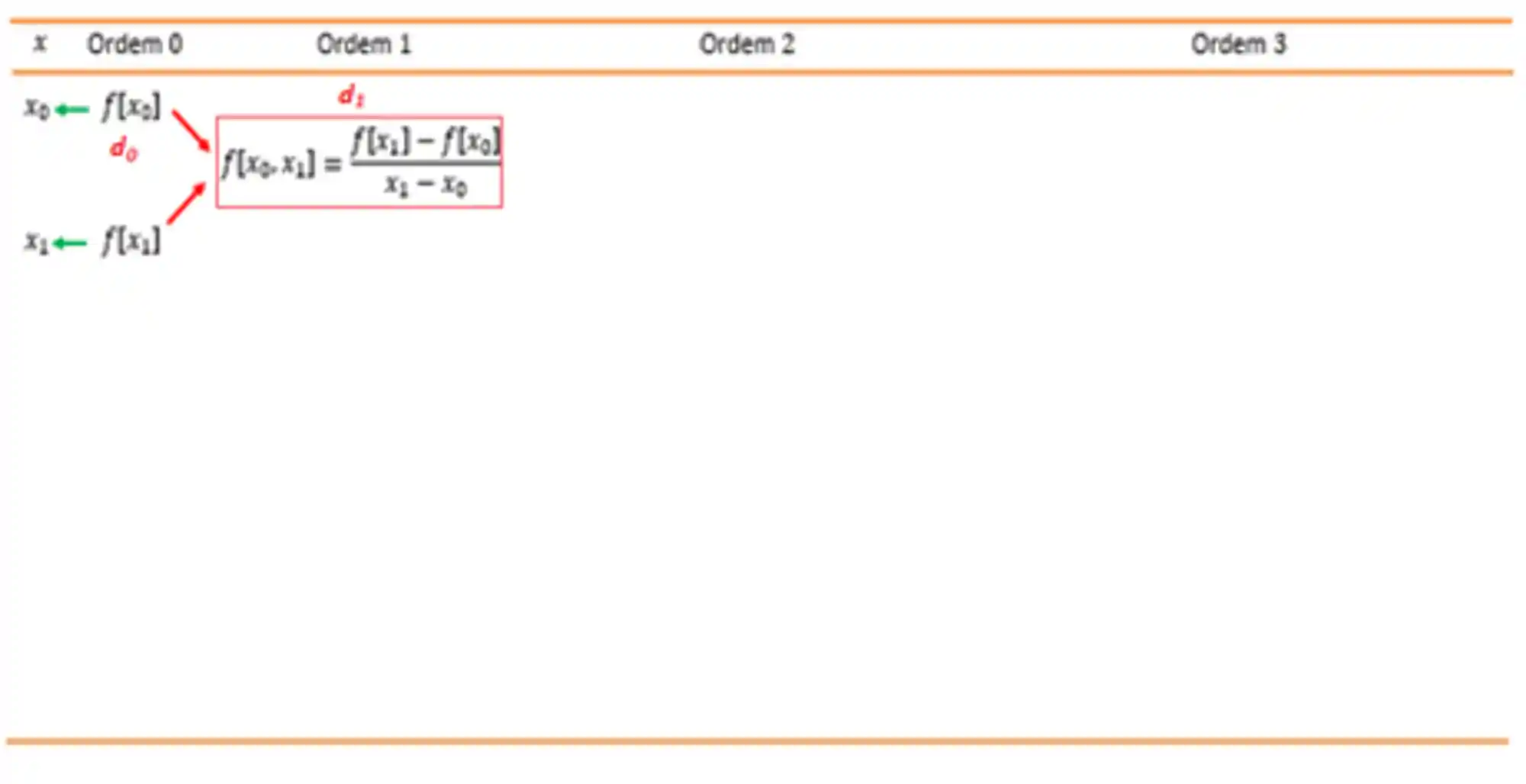
Interpolação de Newton: d1
Interpolação de Newton: d1

Para achar o valor de , vamos completar a tabela fazendo a diferença duas vezes:

Interpolação de Newton: Cálculo de d2
Interpolação de Newton: Cálculo de d2

Continuando esse processo e encontrando as diferenças dívidas, os valores de serão sempre os primeiros de cada nova coluna, ou seja, se quisermos o valor de d_3queremos o primeiro valor da diferença da tabela na coluna de ordem 3, assim por diante:

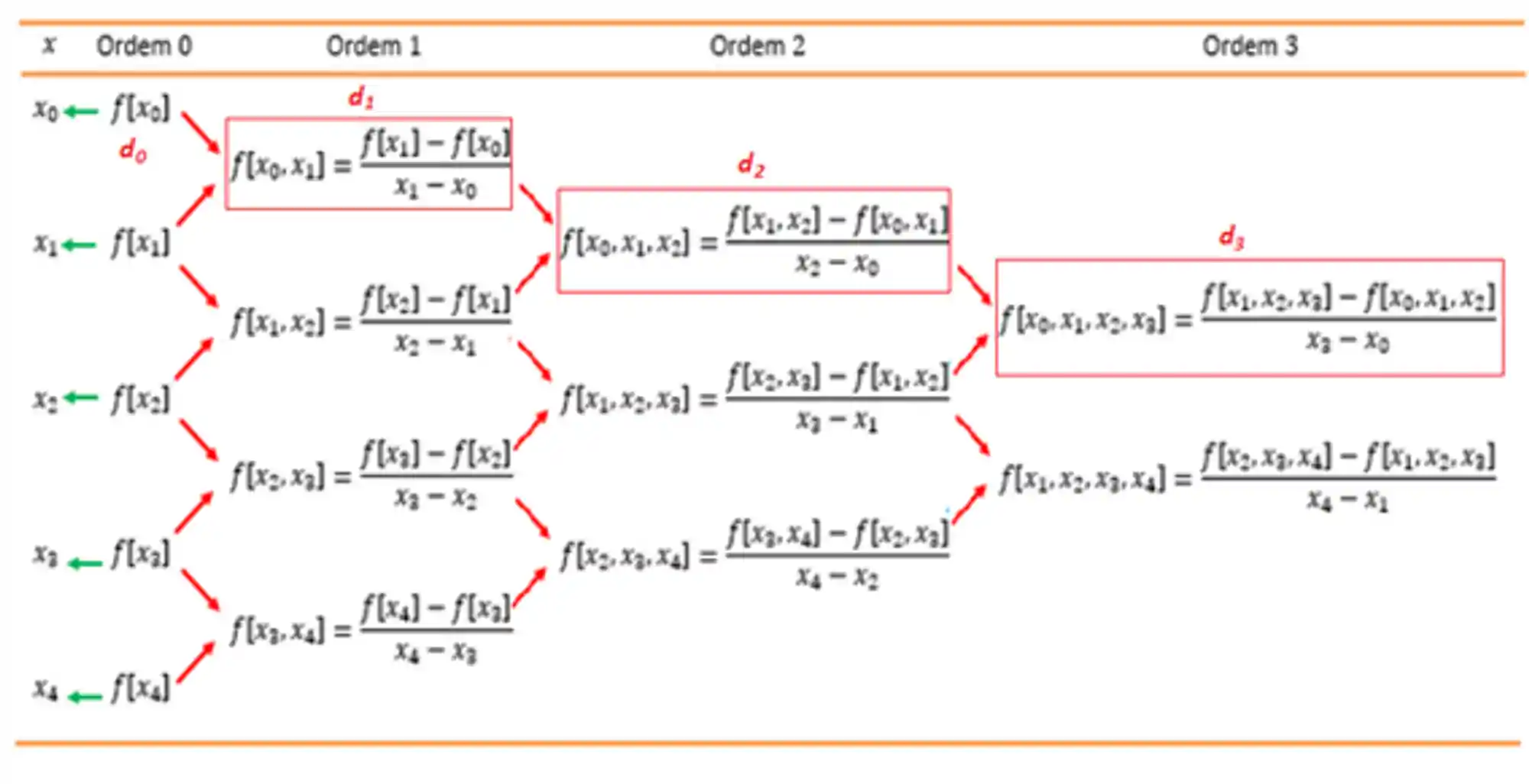
Interpolação de Newton: Cálculo de dn
Interpolação de Newton: Cálculo de dn

Escolhendo do Grau do Polinômio Interpolador

A tabela de diferenças divididas vai nos ajudar na escolha do grau do polinômio! Com a tabela pronta, precisamos analisar as diferenças de cada ordem. Se as diferenças divididas de uma ordem qualquer forem praticamente constantes, ou se as diferenças de ordem forem muito próximas de , então um polinômio interpolador de grau será o que dará a melhor aproximação da função na região considerada.

Vamos ver por exemplo, observe a tabela abaixo com os pontos da função que queremos interpolar:

Dados de entrada do exemplo
Dados de entrada do exemplo

Fazendo a tabela de diferenças divididas e fazendo as continhas, como já demonstrado anteriormente, fica assim:

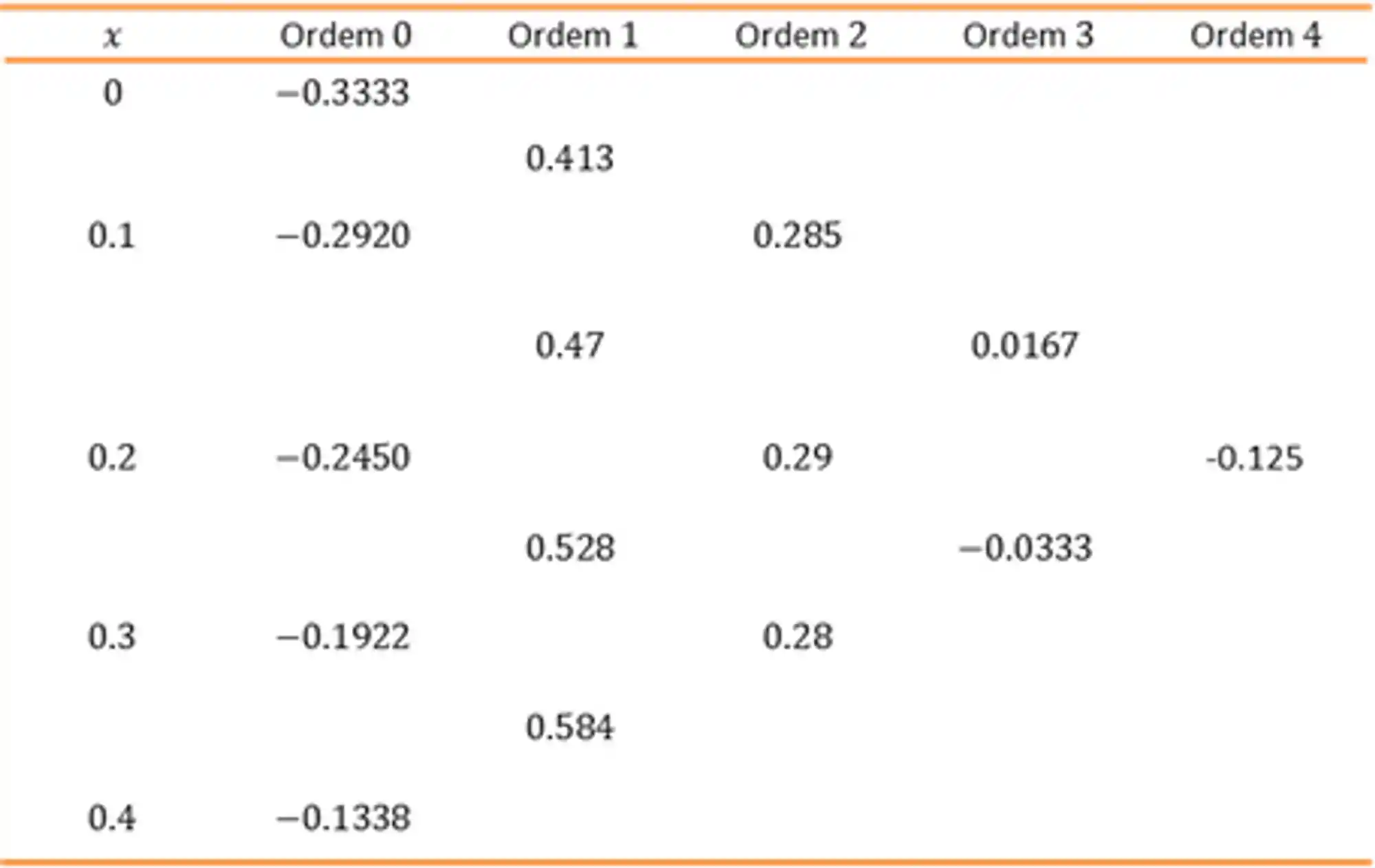
tabela de diferenças divididas para a escolha do grau do polinômio interpolador do exemplo
tabela de diferenças divididas para a escolha do grau do polinômio interpolador do exemplo

Com os valores dessa tabela, podemos encontrar um polinômio de até grau , pois temos o valor de ) mas repare nas diferenças de ordem 2. Percebe que os valores encontrados são quase constantes?

E as de Ordem 3 são bem próximas de 0? Isso quer dizer que a melhor aproximação para no intervalo é um polinômio de grau 2. Ficando com:

Algoritmo

Antes de qualquer coisa, precisamos definir como sendo o operador diferença dividida onde é o mesmo do de maior envolvido e j é a ordem do operador. Por exemplo, seria já que o maior dos é o e ele é de ordem . Teríamos algo desse tipo:

Ordem do polinômio interpolador
Ordem do polinômio interpolador

Assim:

Definido isso, o algoritmo é dado dessa forma:

Passo 1: Dados iniciais

Nessa etapa a gente insere os seguintes dados no programa:

  • Vetor de valores ;
  • Vetor de valores ;
  • Valor onde se quer avaliar .

Passo 2: Para de a repita o passo .

Aqui a gente entra no primeiro looping.

Passo 3: Para de a repita o passo .

Mais um looping;

Passo 4: Calcule ;

Onde é dado por:

Passo 4: A aproximação para será dada por:

Agora vamos praticar com exercícios?

Algoritmo

Exercícios Resolvidos

Exercício Resolvido #1

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 135, exercício 17

Para uma função f , a tabela de diferenças divididas é dada por:

Determine as entradas que estão faltando na tabela.

Passo 1

Temos que:

f x 0 , x 1 , x 2 = f x 1 , x 2 - f x 0 , x 1 x 2 - x 0 = 10 - f x 0 , x 1 0.7 = 50 7

f x 0 , x 1 = 5

f x 1 , x 2 = f x 2 - f x 1 x 2 - x 1 = 6 - f x 1 0.3 = 10

f x 1 = 3

f x 0 , x 1 = f x 1 - f x 0 x 1 - x 0 = 3 - f x 0 0.4 = 5

f x 0 = 1

Resposta

f x 0 = 1  

f x 1 = 3

f x 0 , x 1 = 5

Exercício Resolvido #2

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 134, exercício 10

Mostre que o polinômio interpolador da tabela abaixo é de grau 3 :

Passo 1

-

Vamos começar montando a tabela de diferenças divididas:

Com isso, podemos ver que a partir da ordem 4 , temos apenas 0 na nossa tabela. Isso implica que o polinômio tem grau 3 .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

Lista 6 – Professora Susana – Questão 9

Os seguintes dados correspondem a um polinômio de grau ≤ 5 . Qual é o grau do polinômio?

Passo 1

Montando a tabela de diferenças divididas:

Com isso, podemos ver que a partir da ordem 4 , temos apenas 0 na nossa tabela. Isso implica que o polinômio tem grau 3 .

Resposta

Grau 3

Exercício Resolvido #4

Lista 4 – Professora Angela – UFRJ – Questão 1

Dada a tabela da população de uma vila no início de cada ano, estimar a população na metade de 1973 , usando o polinômio de Newton.

Passo 1

Vamos começar com a tabela de diferenças divididas:

Com isso, sabemos que vamos usar um polinômio de grau 2 dado por:

p 2 x = d 0 + d 1 x - x 0 + d 2 x - x 0 x - x 1

Agora precisamos escolher x 0 , x 1 e x 2 da melhor forma possível. Como queremos a população na metade de 1973 , vamos usar:

x 0 = 1972

x 1 = 1973

x 2 = 1974

E temos:

d 0 = 6600

d 1 = 600

d 2 = 100

Logo,

p 2 x = 6600 + 600 x - 1972 + 100 x - 1972 x - 1973

p 2 x = 100 x 2 - 393900 x + 387899000

Passo 2

Substituindo o valor 1973.5 já que ele quer o valor na metade de 1973 :

p 2 1973.5 = 7575

Resposta

A população dessa vila na metade de 1973 era aproximadamente 7575 pessoas.

Exercício Resolvido #5

Lista de Interpolação – UNICAMP – Questão 8

Encontre aproximações para f 2 , 5 usando polinômios interpoladores de Newton de graus 2 , 3 e 4 usando os dados abaixo:

Passo 1

Montamos a tabela de diferenças divididas:

Passo 2

Um polinômio de grau 2 requer 3 valores x i . Como queremos uma aproximação em x = 2 , 5 usamos:

x 0 = 2,2

x 1 = 2,4

x 2 = 2,6

E temos:

d 0 = 0,5207843

d 1 = - 0,051848

d 2 = - 0,23393125

Nosso p 2 x será:

p 2 x = 0,5207843 - 0,051848 x - 2,2 - 0,23393125 x - 2,2 x - 2,4

p 2 x = - 0,233931 x 2 + 1,02424 x - 0,600307

Aproximando no nosso ponto de interesse:

p 2 2,5 = 0,498224

Passo 3

Já um polinômio de grau 3 requer 4 valores x i . Então usamos:

x 0 = 2,2

x 1 = 2,4

x 2 = 2,6

x 3 = 2,8

E temos:

d 0 = 0,5207843

d 1 = - 0,051848

d 2 = - 0,23393125

d 3 = 0,04966667

Nosso p 3 x será:

p 3 x = 0,5207843 - 0,051848 x - 2,2 - 0,23393125 x - 2,2 x - 2,4 + 0,04966667 x - 2,2 x - 2,4 x - 2,6

p 3 x = 0,0496667 x 3 - 0,591531 x 2 + 1,88049 x - 1 , 28213

Aproximando no nosso ponto de interesse:

p 3 2,5 = 0,498 063

Passo 4

E por último, um polinômio de grau 4 requer 5 valores x i . Então usamos:

x 0 = 2

x 1 = 2,2

x 2 = 2,4

x 3 = 2,6

x 4 = 2,8

E temos:

d 0 = 0,5103757

d 1 = 0,052043

d 2 = - 0,2597275

d 3 = 0,04299375

d 4 = 0,008341146

Nosso p 4 x será:

p 4 x = 0,5103757 + 0,052043 x - 2 - 0,2597275 x - 2 x - 2 , 2 + 0,04299375 x - 2 x - 2 , 2 x - 2 , 4 + 0,008341146 x - 2 x - 2,2 x - 2,4 x - 2,6

p 4 x = 0.00834115 x 4 - 0.0337448 x 3 - 0.279572 x 2 + 1.36334 x - 0.961511

Aproximando no nosso ponto de interesse:

p 4 2,5 = 0,4980 7

Resposta

p 2 2,5 = 0,498224

p 3 2,5 = 0,498063

p 4 2,5 = 0,49807

Exercício Resolvido #6

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 134, exercício 7 adaptada

Encontre o polinômio de interpolação de grau 3 para os pontos da tabela abaixo:

Adicione o ponto f 0.35 = 0.97260 na tabela, e construa um polinômio interpolador de grau 4 .

Passo 1

Montamos a tabela de diferenças divididas (vamos montar já com o ponto extra):

O que está em cima da linha azul é relativo a primeira parte do exercício. O que está abaixo da linha azul é pra segunda parte.

Passo 2

Temos:

x 0 = - 0.1

x 1 = 0.0

x 2 = 0.2

x 3 = 0.3

E da tabela tiramos que:

d 0 = 5.3

d 1 = - 33

d 2 = 129.8333

d 3 = - 556.6667

Nosso p 3 x será:

p 3 x = 5.3 - 33 x - - 0.1 + 129.8333 x - - 0.1 x - 0 - 556.6667 x - - 0.1 x - 0 x - 0.2

p 3 x = - 556.667 x 3 + 185.5 x 2 - 8.8834 x + 2

Passo 3

Vamos ter quase a mesma coisa, mas aparece um x 4 e um d 4 agora:

x 0 = - 0.1

x 1 = 0.0

x 2 = 0.2

x 3 = 0.3

x 4 = 0.35

E da tabela tiramos que:

d 0 = 5.3

d 1 = - 33

d 2 = 129.8333

d 3 = - 556.6667

d 4 = 2730.2434

Nosso p 4 x será:

p 4 x = 5.3 - 33 x - - 0.1 + 129.8333 x - - 0.1 x - 0 - 556.6667 x - - 0.1 x - 0 x - 0.2 + 2730.2434 x - - 0.1 x - 0 x - 0.2 x - 0.3

p 4 x = 2730.24 x 4 - 1648.76 x 3 + 212.802 x 2 + 7.49812 x + 2

Resposta

p 3 x = - 556.667 x 3 + 185.5 x 2 - 8.8834 x + 2

p 4 x = 2730.24 x 4 - 1648.76 x 3 + 212.802 x 2 + 7.49812 x + 2

Exercício Resolvido #7

Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 231, exemplo 7 adaptado.

Dada a tabela abaixo, obtenha o l n ⁡ ( 3.7 ) usando um polinômio de 1º grau

Passo 1

A primeira coisa que a gente precisa fazer é construir a tabela de diferenças divididas, então partiu!!!

A primeira coluna da tabela será composta pelos valores de x . Já a segunda coluna, que recebe o nome de ordem 0, é composta pelos valores da f ( x ) .

Bora achar esses F i , j para as difereças de ordem 1

F 1,1 = f x 1 - f ( x 0 ) x 1 - x 0 =   0.6931 - 0 2 - 1 = 0.6931

F 2,1 = f x 2 - f ( x 1 ) x 2 - x 1 =   1.0986 - 0.6931 3 - 2 = 0.4055

F 3,1 = f x 3 - f ( x 2 ) x 3 - x 2 =   1.3863 - 1.0986 4 - 3 = 0.2877

Colocando na tabela de diferenças

Como o professor nos pediu pra ajustar por uma reta, então basta ir até a ordem 1, nem precisa ir adiante não.

Passo 2

Tá mas que que eu faço agora com esse monte de números que achamos?

Precisamos achar o ln ⁡ 3.7 , olhando pra tabela 3.7 tá dentro do intervalo [3,4]. Então vamo utilizar como d 0 = 1.0986 e d 1 = 0.2877

Nesse nosso exercício, x 0 = 3 já que ele é o primeiro valor tabelado do intervalo que a gente tá interessado.

P 1 ( x ) = d 0 + d 1 ( x - x 0 )

P 1 x = 1.0986 + 0.2877 ( x - 3 )

Passo 3

Já que este polinômio aproxima a f ( x ) , a gente pode escrever o seguinte

f x = 3.7 ≈ P 1 x = 3.7 = 1.0986 + 0.2877 ( 3.7 - 3 )

= 1.3

Resposta

f x = 3.7 ≈ P 1 x = 3.7 = 1.3

Exercício Resolvido #8

Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 234, exemplo 8 adaptado.

Seja f x = e x + x - 1 tabelada e dada abaixo. Obter f ( 0.7 ) por interpolação linear.

Passo 1

A primeira coisa que a gente precisa fazer é construir a tabela de diferenças divididas, então partiu!!!

Como vamos fazer uma interpolação linear (usando uma reta), só precisamos das difereças de ordem 1.

Bora achar esses F i , j para as difereças de ordem 1

F 1,1 = f x 1 - f ( x 0 ) x 1 - x 0 =   1.1487 - 0 0.5 - 0 = 2.2974

F 2,1 = f x 2 - f ( x 1 ) x 2 - x 1 =   2.7183 - 1.1487 1 - 0.5 = 3.1392

F 3,1 = f x 3 - f ( x 2 ) x 3 - x 2 =   4.9811 - 2.7183 1.5 - 1 = 4.5256

F 4,1 = f x 4 - f ( x 3 ) x 4 - x 3 =   8.3890 - 4.9811 2 - 1.5 = 6.8158

Colocando na tabela de diferenças

Como o professor nos pediu pra ajustar por uma reta, então basta ir até a ordem 1, nem precisa ir adiante não.

Passo 2

E agora josé?

Precisamos achar o f ( 0.7 ) , olhando pra tabela 0.7 tá dentro do intervalo [0.5,1]. Então vamo utilizar como d 0 = 1.1487 e d 1 = 3.1392

Nesse nosso exercício, x 0 = 0.5 já que ele é o primeiro valor tabelado do intervalo que a gente tá interessado.

P 1 ( x ) = d 0 + d 1 ( x - x 0 )

P 1 x = 1.1487 + 3.1392 ( x - 0.5 )

Passo 3

Já que este polinômio aproxima a f ( x ) , a gente pode escrever o seguinte

f x = 0.7 ≈ P 1 x = 0.7 = 1.1487 + 3.1392 ( 0.7 - 0.5 )

= 1.7765

Resposta

f x = 0.7 ≈ P 1 x = 0.7 = 1.7765

Exercícios de Livros Relacionados

Sabendo-se que a equação x - e - x = 0 admite uma raiz no intervalo (0, 1), determine o valor desta raiz usando interpolação quadrática. Estime o erro cometido, se possível. Justifique!
Consideremos o problema de interpolação para sen(x), numa tabela de pontos igualmente espaçados com intervalo h, usando um polinômio de 2º grau. Fazendo x 0 =- h ,x 1 = 0 ,x 2 = h , mostre que: | E (
14. Seja p n ( x ) o polinômio de grau ≤ n que interpola f ( x ) em x 0 , x 1 ,... x n escrito na forma de Newton.a) Escreva um algoritmo para avaliar p n ( x - ) , x - ∈ [ x 0 , x n ] semelhante ao a
9. Construa a tabela de diferenças divididas com os dadosa) Estime o valor de f ( 1.23 ) da melhor maneira possível, de forma que se possa estimar o erro cometido.b) Justifique o grau do polinômio que
Seja f ( x )=7 x 5 -3 x 2 -1 . a) Calcular f ( x ) nos pontos x=0 ;x = ± 1 ;x = ± 2 ;x = ± 3 (usar o algoritmo de Briot-Ruffini). Construir a seguir a tabela segundo os valores crescentes de x ; b) Co