Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 7.Exercícios - Ex. 17

17. Considere a integral

I = ∫ 0 1 e - x 2 d x

a) Estime I pela regra de 1 / 3 de Simpson usando h = 0.25

b) Estime I por Quadratura Gaussiana com 2 pontos

c) Sabendo que o valor exato de I (usando 5 casas decimais) é 0.74682 , pede-se

c1) compare as estimativas obtidas em (a) e ( b ) ;

c2) quantos pontos seriam necessários para que a regra dos Trapézios obtivesse a mesma precisão que a estimativa obtida para I em ( b ) .

Passo 1

a) Vamos usar a regra de 1 / 3   de Simpson!

Bom! Se h = 0.25 , então já podemos construir a tabela dado que...

f x = e - x 2

Fazendo isso, obtemos que...

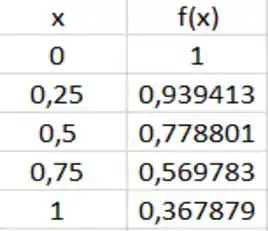
E calculando a integral:

I S = ∫ 0 1 e - x 2 d x = 0.25 3 1 + 4 ⋅ 0.9394 + 0.5697 + 2 ⋅ 0.7788 + 0.36788

I S = 0.746855

Passo 2

b) Agora, vamos pra Quadratura Gaussiana...

Com base na fórmula da mudança dos limites de integração:

x = 1 2 b - a t + a + b

d x = b - a 2 d t

Logo,

I Q = ∫ 0 1 e - x 2 d x = 1 2 ∫ - 1 1 e - t + 1 2 2 d t ≈ 1 2 e - - 3 3 + 1 2 2 + e - 3 3 + 1 2 2

I Q ≅ 0.74659

Passo 3

c) Sabendo que o valor exato com 5 casas decimais é 0.74682 podemos encontrar o erro para a regra de Simpson e a Quadratura Gaussiana:

P a r a   a   R e g r a   d e   1 3   d e   S i m p s o n → ε = 0.746855 - 0.74682 = 3.5 ⋅ 10 - 5

P a r a   a   Q u a d r a t u r a   G a u s s i a n a → ε = 0.74659 - 0.74682 = 2,3 ⋅ 10 - 4

Ou seja! Nesse caso, a regra de 1 / 3 de Simpson acabou se demonstrando mais eficiente!

Passo 4

Quanto ao número de pontos necessários para que a regra dos Trapézios, bora recorrer a fórmula limitante do erro...

Para a regra dos trapézios, como h é dado por...

h = 1 - 0 n = 1 n

Temos que...

1 12 n 2 ⋅ max x ∈ a , b ⁡ f ' ' x ≤ 0.00023

Tirando agora, a 2 ª derivada de f ( x ) ...

f ' ' x = e - x 2 ( 4 x 2 - 2 )

Calculando o valor máximo...

f ' ' 0 = e - x 2 4 x 2 - 2 = 2

f ' ' 1 = e - x 2 4 x 2 - 2 = 0.73576

Podemos ver que ele acontece em x = 0 . Desse modo...

1 12 n 2 ⋅ max x ∈ a , b ⁡ f ' ' x ≤ 0.00023

2 12 n 2 ≤ 0.00023

n ≥ 26.91

Logo, ficamos com n = 27 !

Resposta

a)

I S = 0.746855

b)

I Q ≅ 0.74659

c)

ε ≅ 2,3 ⋅ 10 - 4

n = 27

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios 97 e 98, ache um valor aproximado para a integral, usando a regra do trapézio com n = 4 . Expresse o resultado com até três casas decimais.97. ∫ 0 2 1 + x 2d x
Nos exercícios 99 e 100, ache um valor aproximado para a integral, usando a regra de Simpson com n = 4 . Expresse o resultado com até três casas decimais.99. ∫ 0 2 1 + x 2d x
94. Um automóvel rodando a uma velocidade constante de 80 Km/h por uma estrada reta não obedece um sinal de parada. Se 3s mais tarde o carro da polícia rodoviária estacionado no sinal de parada parte
95. Suponha que num dado dia, numa certa cidade, a temperatura fahrenheit seja f t grus , t horas depois da meia – noite e f t = 60 - 15 s e n 1 12 π 8 - t0 ≤ t ≤ 24 . (a) Faça um esboço do gráfico de
108. Dada F x = ∫ x 2 x 1 t d tex0 . Prove que F é uma função constante , mostrando que F´(x) = 0. (Sugestão: use o primeiro teorema funtamental do cálculo após escrever a integral dada como a diferen