Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Derivação Numérica

Ver Todos os Exercícios

Teoria

Introdução

Fala aí meus consagrados, tudo certinho? Antes de começar a mexer com aquelas EDO´s barra pesada, vamos retomar alguns conceitos importantes que vem láaaa do cálculo 1.

Mas é um assunto molezinha, estamos falando de derivadas.

Fala aí, tu lembras a definição de derivada? Não vale colar... e olha que eu nem estou falando da clássica “derivada representa a taxa de variação”.

Se não lembra, nem esquenta. To falando da definição raiz (que vem láaaa daquelas teorias de limites) hahaha é essa aqui em baixo: f ' x 0 = lim h → 0 ⁡ f x 0 + h - f x 0 h

Então para aproximarmos nossa derivada é só encontrarmos o valor de

f x 0 + h - f x 0 h

usando um h bem pequeno. Pronto, acabou esse tópico.

Ai... Capaaaz que seria tão fácil assim. Vamos partir daquela fórmula pra achar inúmeras ramificações. E agora a brincadeira começa a ficar boa.

Essas ramificações geralmente são obtidas pelo polinômio de Lagrange ou pelo truncamento da série de Taylor. Que, cá entre nós... é a mesmíssima coisa, já que o tal do Lagrange resolvia as coisinhas usando a série de Taylor.

Derivada Primeira

A primeira coisa que vamos fazer aqui é analisar o gráfico. Tá ligado que eu puxei a definição de derivadas usando limites né? Mas, derivação também tem outros conceitos relacionados...

É, estamos falando daquela reta que toca a curva, a famosa tangente.

Então se liga aqui, basicamente o que vai acontecer nessas fórmulas é o seguinte:

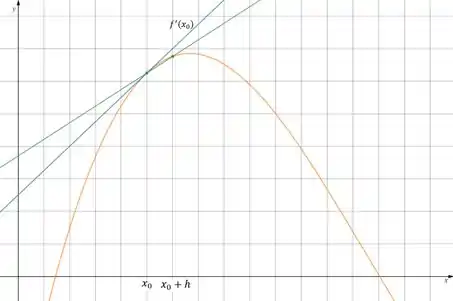
Perceba que quanto menor for o nosso h mais a nossa aproximação (reta verde) se aproxima do valor exato da derivada (reta azul)? Mas, precisamos ter alguns cuidados.

Falei ali em cima que quanto menor o h melhor será nossa aproximação e iremos conseguir computar mais casas decimais.

Opa, espera aí! Tudo tem limite né? Imagine um computador processando essas informações... agora pense que você está cada vez mais reduzindo os intervalos que ele é capaz de computar... Isso quer dizer que quanto menor for o nosso h mais próximo do limite de representação da máquina ele vai chegando.

Então, na real se nós tivermos um h muito pequeno, diminuiremos o erro da aproximação. Maaaaaaaaas aumentaremos muito o erro de arredondamento ou truncamento então não exagere haha.

Dito isso, podemos ver quais são os métodos:

Diferença Avançada:

Se usarmos o polinômio de Taylor de grau 1 ficamos com:

f x ≅ f x 0 + f ' x 0 x - x 0

Sendo uma aproximação é válida para x próximo de x 0 . Vamos fazer a mudança de variáveis x = x 0 + h , sendo uma diferença adiantada... nós vamos adiantar (ou seja, acrescentar) alguns h na conta, obtendo:

f x 0 + h ≅ f x 0 + f ' x 0 x 0 + h - x 0

f x 0 + h ≅ f x 0 + h f ' x 0

f ' x 0 ≅ f x 0 + h - f x 0 h

Diferença Atrasada:

Esse nome é bem sugestivo, se no de diferença adianta nós adicionávamos h , na diferença atrasada fazemos o oposto: subtraímos h .

Ouuuu seja, ao invés de fazermos a substituição x = x 0 + h , fazemos x = x 0 - h , obtendo:

f x 0 - h ≅ f x 0 + f ' x 0 x 0 - h - x 0

f x 0 - h ≅ f x 0 - h f ' x 0

f ' x 0 ≅ f x 0 - f x 0 - h h

Diferença Central:

Já no caso da central temos que encontrar um caminho alternativo para ficar no centro, ou seja, entre as outras duas. Então, esse meio que faz uma média entre as duas. Somando as duas fórmulas ficamos com:

2 f ' x 0 ≅ f x 0 + h - f x 0 h + f x 0 - f x 0 - h h

2 f ' x 0 ≅ f x 0 + h - f x 0 - h h

f ' x 0 ≅ f x 0 + h - f x 0 - h 2 h

Erro na Derivada Primeira

Mas é claro que nosso querido erro não poderia ficar de fora! Se nós estamos fazendo aproximações, significa que precisamos saber o quão perto estamos do valor real.

Para esses casos o limitante do erro pode ser encontrado pela teoria lá de Lagrange ou Taylor também. Para as diferenças atrasada e avançada ele é dado por:

E ≤ h 2 ∙ max x ∈ a , b ⁡ f ' ' x

E para a diferença central temos:

E ≤ h 2 6 ∙ max x ∈ a , b ⁡ f 3 x

Onde a , b é um intervalo que contenha x 0 e x 0 + h para a diferença avançada, x 0 - h e x 0 para a diferença atrasada e x 0 - h e x 0 + h para a diferença central.

Aí você poderia argumentar que não faz muito sentido termos que saber a derivada segunda ou terceira da função para calcular o erro já que para estarmos derivando numericamente provavelmente não queremos calcular a derivada haha.

Eu concordo 100 % com você, mas o professor pode pedir então é sempre bom mencionar.

Exemplo

Bora resolver um exemplo que esse negócio vai ficar mais fácil do que você imagina.

Aproxime o valor da derivada de ln ⁡ x no ponto x 0 = 0.5 usando h = 0.05 pelos três métodos apresentados. Calcule também um limitante para o erro e o erro exato.

Pelo método da diferença avançada:

f ' 0.5 ≅ f 0.55 - f 0.5 0.05 = 1.90620

O limitante do erro é:

E ≤ h 2 ∙ max x ∈ a , b ⁡ f ' ' x

Onde h vale 0.05 . E a derivada segunda de ln ⁡ x é dada por f ' ' x = - 1 x 2 . O módulo máximo dessa função no intervalo 0.5,0.55 ocorre em x = 0.5 e tem como valor f ' ' 0.5 = 4 . Substituindo:

E ≤ 0.05 2 ∙ 4 = 0.1

O erro exato é:

E A = 2 - 1.90620 = 0.0938

Usando diferença atrasada:

f ' 0.5 ≅ f 0.5 - f 0.45 0.05 = 2.10721

Usando a mesma fórmula para o limitante do erro temos que o módulo máximo de f ' ' x no intervalo 0.45,0.5 ocorre em x = 0.45 e tem como valor f ' ' 0.45 = 4.938 . Substituindo:

E ≤ 0.05 2 ∙ 4.938 = 0.12345

O erro exato é:

E A = 2 - 2.10721 = 0.10721

E por último a diferença central:

f ' 0.5 ≅ f 0.55 - f 0.45 0.1 = 2.00671

Agora nossa fórmula para o erro muda um pouquinho. Temos: E ≤ h 2 6 ∙ max x ∈ a , b ⁡ f 3 x

A terceira derivada de ln ⁡ x é f 3 x = 2 x 3 . E o módulo máximo dela no intervalo 0.45,0.55 acontece em x = 0.45 onde temos f 3 0.45 = 21.948 . Substituindo:

E ≤ 0.05 2 6 ∙ 21.948 = 0.009

E o erro exato é:

E A = 2 - 2.00671 = 0.00671

Se juntarmos tudo isso numa tabelinha:

Derivada Segunda

Calma, relaxa que estamos quase acabando . Como faríamos uma aproximação para a derivada segunda de uma função f x avaliada em algum ponto?

Vimos lá em cima que para a derivada de primeira o primeiro polinômio de Lagrange ou o polinômio de Taylor de grau 1 .

No caso da segunda derivada vamos usar até o segundo Polinômio de Lagrange ou o polinômio de Taylor de grau 2 . Fazendo aquelas mesmas substituições x = x 0 + h e x = x 0 - h e reorganizando ficamos com:

f x 0 + h ≅ f x 0 + h f ' x 0 + h 2 f ' ' x 0 2

f x 0 - h ≅ f x 0 - h f ' x 0 + h 2 f ' ' x 0 2

Somando:

f x 0 + h + f x 0 - h ≅ 2 f x 0 + h 2 f ' ' x 0

Isolando a derivada segunda:

f ' ' x 0 ≅ f x 0 + h - 2 f x 0 + f x 0 - h h 2

Ah pode chamar esse método de Diferença Central para a Derivada Segunda.

Booooora fazer exercício!!!

Derivada Primeira

Erro na Derivada Primeira

Exemplo

Derivada Segunda

Exercícios Resolvidos

Exercício Resolvido #1

UFAL – Professor Eduardo Toledo de Lima Junior. (ADAPTADO)

Usando a fórmula mais acurada, determine a aceleração no tempo 1,5 s :

Passo 1

Bom, esse é um exercício inicial do assunto, então é bem tranquilo. A dificuldade vai aumentando com o passar dos exercícios. Vamos lá!

A fórmula mais acurada é das diferenças centradas, que é:

f ' x 0 = f x 0 + h - f ( x 0 - h ) 2 h

De acordo com os valores tabelados, percebemos que h = 0,5 , já que os valores de t espaçam 0,5 s entre si.

Como queremos a aceleração no ponto 1,5 s , precisamos encontrar a derivada nesse ponto. Então vamos apenas aplicar essa fórmula.

Passo 2

No ponto x = 1,5 s :

f ' 1,5 = f 1,5 + 0,5 - f ( 1,5 - 0,5 ) ( 2 ) ( 0,5 )

Resolvendo essa equação:

f ' 1,5 = 4,52 - 1,25 ( 2 ) ( 0,5 ) = 3,27

Resposta

f ' 1,5 = 3.27

Exercício Resolvido #2

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 182, exercício 3

Os dados do último exercício foram tirados das funções abaixo. Calcule o erro absoluto das suas aproximações do exercício 1 e encontre limitantes para o erro.

a f x = sin ⁡ x

b f x = e x - 2 x 2 + 3 x - 1

Passo 1

a Relembrando as aproximações que encontramos no último exercício:

f ' 0.5 ≅ 0.852

f ' 0.6 ≅ 0.796

f ' 0.7 ≅ 0.796

O valor exato vai ser:

f x = sin ⁡ x

f ' x = cos ⁡ x

f ' 0.5 = 0.87758

f ' 0.6 = 0.82534

f ' 0.7 = 0.76484

E A f ' 0.5 = 0.852 - 0.87758 = 0.02558

E A f ' 0.6 = 0.796 - 0.82534 = 0.02934

E A f ' 0.7 = 0.796 - 0.76484 = 0.03116

Passo 2

Agora temos que encontrar o limitante para o erro usando a fórmula

E ≤ h 2 ∙ max x ∈ a , b ⁡ f ' ' x

Onde f ' ' x = - sin ⁡ x e tem seu módulo máximo no intervalo 0.5,0.6 em x = 0.6 e seu módulo máximo no intervalo 0.6,0.7 em x = 0.7 :

f ' ' 0.6 = 0.56464

f ' ' 0.7 = 0.64422

Substituindo nas fórmulas:

E A f ' 0.5 ≤ 0.1 2 ∙ 0.56464 = 0.028232

E A f ' 0.6 ≤ 0.1 2 ∙ 0.64422 = 0.032211

E A f ' 0.7 ≤ 0.1 2 ∙ 0.64422 = 0.032211

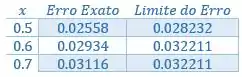
Passo 3

Organizando numa tabelinha:

Passo 4

b As aproximações que encontramos no último exercício foram:

f ' 0 ≅ 3.707

f ' 0.2 ≅ 3.152

f ' 0.4 ≅ 3.152

O valor exato vai ser:

f x = e x - 2 x 2 + 3 x - 1

f ' x = e x - 4 x + 3

f ' 0 = 4

f ' 0.2 = 3.4214

f ' 0.4 = 2.8918

E A f ' 0 = 3.707 - 4 = 0.293

E A f ' 0.2 = 3.152 - 3.4214 = 0.2694

E A f ' 0.4 = 3.152 - 2.8918 = 0.2602

Passo 5

Agora vamos encontrar o limitante para o erro usando a fórmula

E ≤ h 2 ∙ max x ∈ a , b ⁡ f ' ' x

Onde f ' ' x = e x - 4 e tem seu módulo máximo no intervalo 0,0.2 em x = 0 e seu módulo máximo no intervalo 0.2,0.4 em x = 0.2 :

f ' ' 0 = 3

f ' ' 0.2 = 2.7786

Substituindo nas fórmulas:

E A f ' 0 ≤ 0.2 2 ∙ 3 = 0.3

E A f ' 0.2 ≤ 0.2 2 ∙ 2.7786 = 0.27786

E A f ' 0.4 ≤ 0.2 2 ∙ 2.7786 = 0.27786

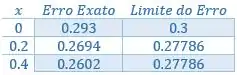
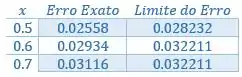
Passo 6

Organizando numa tabelinha:

Resposta

a

b

Exercício Resolvido #3

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 182, exercício 1

Usando as fórmulas de diferença avançada e diferença atrasada determine os valores que estão faltando nas tabelas abaixo:

Passo 1

Para o primeiro valor da tabela nós só podemos usar a diferença avançada assim como para o último só podemos usar a diferença atrasada.

Para o do meio podemos usar qualquer um dos dois. Eu vou escolher a diferença avançada mesmo.

a

f ' 0.5 ≅ f 0.6 - f 0.5 0.1 = 0.5646 - 0.4794 0.1 = 0.852

f ' 0.6 ≅ f 0.7 - f 0.6 0.1 = 0.6442 - 0.5646 0.1 = 0.796

f ' 0.7 ≅ f 0.7 - f 0.6 0.1 = 0.6442 - 0.5646 0.1 = 0.796

Repare que as aproximações de f ' 0.7 e de f ' 0.6 ficaram iguais! Isso porque escolhemos o método da diferença avançada para f ' 0.6 .

Se tivéssemos escolhido o método da diferença atrasada os valores de f ' 0.5 e de f ' 0.6 teriam sido os mesmos.

Passo 2

b

f ' 0 ≅ f 0.2 - f 0 0.2 = 0.7414 - 0 0.2 = 3.707

f ' 0.2 ≅ f 0.4 - f 0.2 0 . 2 = 1.3718 - 0.7414 0 . 2 = 3.152

f ' 0 . 4 ≅ f 0.4 - f 0.2 0.2 = 1.3718 - 0.7414 0.2 = 3.152

Resposta

a

f ' 0.5 ≅ 0.852

f ' 0.6 ≅ 0.796

f ' 0.7 ≅ 0.796

b

f ' 0 ≅ 3 . 707

f ' 0.2 ≅ 3.152

f ' 0.4 ≅ 3.152

Exercício Resolvido #4

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 182, exercício 3

Os dados do último exercício foram tirados das funções abaixo. Calcule o erro absoluto das suas aproximações do exercício 1 e encontre limitantes para o erro.

a f x = sin ⁡ x

b f x = e x - 2 x 2 + 3 x - 1

Passo 1

a Relembrando as aproximações que encontramos no último exercício:

f ' 0.5 ≅ 0.852

f ' 0.6 ≅ 0.796

f ' 0.7 ≅ 0.796

O valor exato vai ser:

f x = sin ⁡ x

f ' x = cos ⁡ x

f ' 0.5 = 0.87758

f ' 0.6 = 0.82534

f ' 0.7 = 0.76484

E A f ' 0.5 = 0.852 - 0.87758 = 0.02558

E A f ' 0.6 = 0.796 - 0.82534 = 0.02934

E A f ' 0.7 = 0.796 - 0.76484 = 0.03116

Passo 2

Agora temos que encontrar o limitante para o erro usando a fórmula

E ≤ h 2 ∙ max x ∈ a , b ⁡ f ' ' x

Onde f ' ' x = - sin ⁡ x e tem seu módulo máximo no intervalo 0.5,0.6 em x = 0.6 e seu módulo máximo no intervalo 0.6,0.7 em x = 0.7 :

f ' ' 0.6 = 0.56464

f ' ' 0.7 = 0.64422

Substituindo nas fórmulas:

E A f ' 0.5 ≤ 0.1 2 ∙ 0.56464 = 0.028232

E A f ' 0.6 ≤ 0.1 2 ∙ 0.64422 = 0.032211

E A f ' 0.7 ≤ 0.1 2 ∙ 0.64422 = 0.032211

Passo 3

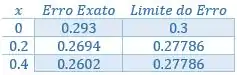
Organizando numa tabelinha:

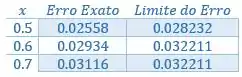
Passo 4

b As aproximações que encontramos no último exercício foram:

f ' 0 ≅ 3.707

f ' 0.2 ≅ 3.152

f ' 0.4 ≅ 3.152

O valor exato vai ser:

f x = e x - 2 x 2 + 3 x - 1

f ' x = e x - 4 x + 3

f ' 0 = 4

f ' 0.2 = 3.4214

f ' 0.4 = 2.8918

E A f ' 0 = 3.707 - 4 = 0.293

E A f ' 0.2 = 3.152 - 3.4214 = 0.2694

E A f ' 0.4 = 3.152 - 2.8918 = 0.2602

Passo 5

Agora vamos encontrar o limitante para o erro usando a fórmula

E ≤ h 2 ∙ max x ∈ a , b ⁡ f ' ' x

Onde f ' ' x = e x - 4 e tem seu módulo máximo no intervalo 0,0.2 em x = 0 e seu módulo máximo no intervalo 0.2,0.4 em x = 0.2 :

f ' ' 0 = 3

f ' ' 0.2 = 2.7786

Substituindo nas fórmulas:

E A f ' 0 ≤ 0.2 2 ∙ 3 = 0.3

E A f ' 0.2 ≤ 0.2 2 ∙ 2.7786 = 0.27786

E A f ' 0.4 ≤ 0.2 2 ∙ 2.7786 = 0.27786

Passo 6

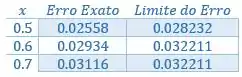
Organizando numa tabelinha:

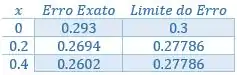
Resposta

a

b

Exercício Resolvido #5

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 182, exercício 5 adaptado

Use a fórmula mais acurada para determinar os valores que estão faltando nas tabelas abaixo:

Passo 1

Vamos fazer o seguinte: para o primeiro valor da tabela nós só podemos usar a diferença avançada assim como para o último só podemos usar a diferença atrasada. Para os dois do meio usamos a diferença central que normalmente é mais acurada.

a

f ' 1.1 ≅ f 1.2 - f 1.1 0.1 = 19.98167

f ' 1.2 ≅ f 1.3 - f 1.1 0 . 2 = 22.19364

f ' 1.3 ≅ f 1 . 4 - f 1 . 2 0.2 = 27.10735

f ' 1.4 ≅ f 1 . 4 - f 1 . 3 0.1 = 29.8091

Passo 2

b

f ' 8.1 ≅ f 8.3 - f 8 . 1 0 . 2 = 3.1041

f ' 8.3 ≅ f 8.5 - f 8.1 0 . 4 = 3.11615

f ' 8.5 ≅ f 8.7 - f 8.3 0 . 4 = 3.14

f ' 8.7 ≅ f 8.7 - f 8.5 0 . 2 = 3.15175

Resposta

a

f ' 1.1 ≅ 19.98167

f ' 1.2 ≅ 22.19364

f ' 1.3 ≅ 27.10735

f ' 1.4 ≅ 29.8091

b

f ' 8.1 ≅ 3.1041

f ' 8.3 ≅ 3.11615

f ' 8.5 ≅ 3.14

f ' 8.7 ≅ 3.15175

Exercício Resolvido #6

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 183, exercício 7

Os dados do último exercício foram tirados das funções abaixo. Calcule o erro absoluto das suas aproximações do exercício 3 e encontre limitantes para o erro.

a f x = e 2 x

b f x = x ln ⁡ x

Passo 1

a Relembrando as aproximações que encontramos no último exercício:

f ' 1.1 ≅ 19.98167

f ' 1.2 ≅ 22.19364

f ' 1.3 ≅ 27.10735

f ' 1.4 ≅ 29.8091

O valor exato vai ser:

f x = e 2 x

f ' x = 2 e 2 x

f ' 1.1 = 18.05

f ' 1.2 = 22.0464

f ' 1.3 = 26.9275

f ' 1.5 = 32.8893

E A f ' 1.1 = 19.98167 - 18.05 = 1.93167

E A f ' 1.2 = 22.19364 - 22.0464 = 0.14724

E A f ' 1.3 = 27.10735 - 26.9275 = 0.17985

E A f ' 1.4 = 29.8091 - 32.8893 = 3.0802

Repare que os erros obtidos na diferença avançada e atrasada foram mais de 10 vezes maiores que os erros obtidos na diferença central.

Passo 2

Agora temos que encontrar o limitante para o erro usando a fórmula:

E ≤ h 2 ∙ max x ∈ a , b ⁡ f ' ' x

para as fórmulas da diferença avançada e atrasada e a fórmula

E ≤ h 2 6 ∙ max x ∈ a , b ⁡ f 3 x

para a diferença central. Temos que:

f ' ' x = 4 e 2 x

f 3 x = 8 e 2 x

E disso tiramos os valores dos máximos necessários:

max x ∈ 1.1,1.2 ⁡ 4 e 2 x = 4 e 2 1.2 = 44.0927

max x ∈ 1.1,1.3 ⁡ 8 e 2 x = 8 e 2 1.3 = 107.710

max x ∈ 1.2,1.4 ⁡ 8 e 2 x = 8 e 2 1.4 = 131.557

max x ∈ 1.3,1.4 ⁡ 4 e 2 x = 4 e 2 1.4 = 65.7786

Substituindo nas fórmulas:

E A f ' 1.1 ≤ 0.1 2 ∙ 44.0927 = 2.204635

E A f ' 1.2 ≤ 0.2 2 6 ∙ 107.710 = 0.718067

E A f ' 1.3 ≤ 0.2 2 6 ∙ 131.557 = 0.877047

E A f ' 1.4 ≤ 0.1 2 ∙ 65.7786 = 3.28893

Passo 3

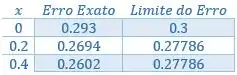
Organizando numa tabelinha:

Passo 4

b As aproximações do último exercício foram:

f ' 8.1 ≅ 3.1041

f ' 8.3 ≅ 3.11615

f ' 8.5 ≅ 3.14

f ' 8.7 ≅ 3.15175

O valor exato vai ser:

f x = x ln ⁡ x

f ' x = ln ⁡ x + 1

f ' 8.1 = 3.09186

f ' 8.3 = 3.11626

f ' 8.5 = 3.14007

f ' 8.7 = 3.16332

E A f ' 8 . 1 = 3.1041 - 3.09186 = 0.01224

E A f ' 8.3 = 3.11615 - 3.11626 = 0.00011

E A f ' 8.5 = 3.14 - 3.14007 = 0.00007

E A f ' 8.7 = 3.15175 - 3.16332 = 0.01157

Novamente os erros obtidos na diferença avançada e atrasada foram bem maiores que os erros da diferença central. Aproximadamente 100 vezes maiores dessa vez haha.

Passo 5

Agora temos que encontrar o limitante para o erro usando a fórmula:

E ≤ h 2 ∙ max x ∈ a , b ⁡ f ' ' x

para as fórmulas da diferença avançada e atrasada e a fórmula

E ≤ h 2 6 ∙ max x ∈ a , b ⁡ f 3 x

para a diferença central. Temos que:

f ' ' x = 1 x

f 3 x = - 1 x 2

E disso tiramos os valores dos máximos necessários:

max x ∈ 8.1,8.3 ⁡ 1 x = 1 8.1 = 0.123457

max x ∈ 8.1,8.5 ⁡ - 1 x 2 = 1 8.1 2 = 0.015242

max x ∈ 8.3,8.7 ⁡ - 1 x 2 = 1 8 . 3 2 = 0.014516

max x ∈ 8.5,8.7 ⁡ 1 x = 1 8 . 5 = 0.117647

Substituindo nas fórmulas:

E A f ' 8.1 ≤ 0 . 2 2 ∙ 0.123457 = 0.012346

E A f ' 8.3 ≤ 0 . 4 2 6 ∙ 0.015242 = 0.000406

E A f ' 8.5 ≤ 0 . 4 2 6 ∙ 0.014516 = 0.000387

E A f ' 8.7 ≤ 0 . 2 2 ∙ 0.117647 = 0.011765

Passo 6

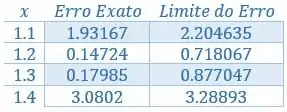
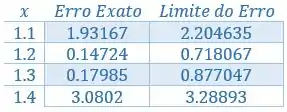
Organizando numa tabelinha:

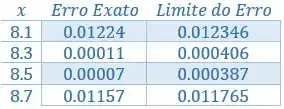
Resposta

a

b

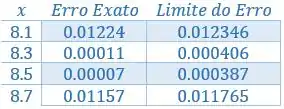
Exercício Resolvido #7

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 184, exercício 18

Considere a tabela abaixo:

a Use todas as fórmulas desse tópico para aproximar f ' 0.4 e f ' ' 0.4 .

b Use todas as fórmulas desse tópico para aproximar f ' 0.6 e f ' ' 0.6 .

Passo 1

a Diferença Avançada:

f ' 0.4 ≅ f 0.6 - f 0.4 0.2 = - 0.548665

Diferença Atrasada:

f ' 0.4 ≅ f 0 . 4 - f 0 . 2 0.2 = - 0.310471

Diferença Central:

f ' 0.4 ≅ f 0.6 - f 0.2 0.4 = - 0.429568

Diferença Central para a Segunda Derivada:

f ' ' 0.4 ≅ f 0.6 - 2 f 0.4 + f 0.2 0.2 2 = - 1.19097

Passo 2

b Diferença Avançada:

f ' 0 . 6 ≅ f 0 . 8 - f 0 . 6 0.2 = - 0.847144

Diferença Atrasada:

f ' 0 . 6 ≅ f 0.6 - f 0.4 0.2 = - 0.548665

Diferença Central:

f ' 0 . 6 ≅ f 0 . 8 - f 0 . 4 0.4 = - 0 . 697904

Diferença Central para a Segunda Derivada:

f ' ' 0 . 6 ≅ f 0 . 8 - 2 f 0 . 6 + f 0 . 4 0.2 2 = - 1.492393

Resposta

a Diferença Avançada:

f ' 0.4 ≅ - 0.548665

Diferença Atrasada:

f ' 0.4 ≅ - 0.310471

Diferença Central:

f ' 0.4 ≅ - 0.429568

Diferença Central para a Segunda Derivada:

f ' ' 0.4 ≅ - 1.19097

b Diferença Avançada:

f ' 0.6 ≅ - 0.847144

Diferença Atrasada:

f ' 0.6 ≅ - 0.548665

Diferença Central:

f ' 0.6 ≅ - 0.697904

Diferença Central para a Segunda Derivada:

f ' ' 0.6 ≅ - 1.492393

Exercício Resolvido #8

2ª lista de exercícios – Derivação Numérica. UNICAMP

Considere os dados na tabela a seguir:

Determine f ' ' ( 0.4 ) e f ' ' ( 0.6 ) . Considere h = 0.2

Passo 1

Faaa aeee, o professor tá te pedindo pra fazer a derivada segunda numérica. A fórmula tava lá no finalzinho da teoria e é essa aqui oh.

f ' ' x 0 = f x 0 + h - 2 * f x 0 + f ( x 0 - h ) h 2

Show de bolinhas, vai ser tranquilo de resolver esse negócio!!

Agora a gente só precisa substituir os valores, blz?

f ' ' 0.4 = f 0.6 - 2 * f 0.4 + f 0.2 h 2

f ' ' 0.4 = 0.808038 - 2 * ( 0.917771 ) + 0.9798652 ( 0.2 ) 2 = - 1.191

f ' ' 0.6 = f 0.8 - 2 * f 0.6 + f 0.4 h 2

f ' ' 0.6 = 0.6386093 - 2 * 0.808038 + 0.917771 ( 0.2 ) 2 = - 1.4923

Resposta

f ' ' ( 0.4 ) = - 1.191

f ' ' 0.6 = - 1.4923

Exercício Resolvido #9

2ª lista de exercícios – Derivação Numérica. UNICAMP - Adaptado

Seja f x = 3 x e x - c o s ⁡ ( x ) . Calcule uma aproximação para f ' ' ( 1.3 ) .

  1. Considere h = 0.1
  2. Considere h = 0.01

Passo 1

Faaa aeee, a primeira coisa que você precisa lembrar é da fórmula da derivada segunda numérica, que tá lá no finalzinho da teoria, e é essa aqui:

f ' ' x 0 = f x 0 + h - 2 * f x 0 + f ( x 0 - h ) h 2

Se a gente prestar bem atenção na fórmula, precisamos da função tabelada em 3 pontos, certo?

Para fazermos a derivada segunda precisamos do valor da f em x 0 , em x 0 + h , e em x 0 - h . Então bora já constuir a tabela do item a e b de uma vez.

Pro item a, com passo h = 0.1 , precisaremos de f ( 1.2 ) , f ( 1.3 ) e f ( 1.4 ) . Já para o caso do item b, vamos precisar de f ( 1.29 ) , f ( 1.30 ) e f ( 1.31 )

Só precisamos agora substituir esses valores de x na f ( x ) que o professor deu no enunciado.

Tabela para o item a:

Tabela para o item b:

Passo 2

Resolvendo o item (a), a gente só precisa agora substituir os valores na fórmula da derivada segunda, blz?

f ' ' 1.3 = f 1.4 - 2 * f 1.3 + f 1.2 h 2

f ' ' 0.4 = 16.86187 - 2 * ( 14.04276 ) + 11.59006 ( 0.1 ) 2 = 36.641

Passo 3

Para o item (b):

f ' ' 1.30 = f 1.31 - 2 * f 1.30 + f 1.29 h 2

f ' ' 0.6 = 14.30741 - 2 * 14.04276 + 13.78176 ( 0.1 ) 2 = 36.5

Resposta

f ' ' ( 1.3 ) = 36.641

f ' ' 1.30 = 36.5

Exercício Resolvido #10

2ª lista de exercícios – Derivação Numérica. UNICAMP - Adaptado

Seja f x = cos ⁡ 3 x 2 - e 2 x . Tabele a função no intervalo [-2.7, -2.1] com passo h = 0.2 e calcule f ' ( x ) para cada ponto da tabela

Passo 1

Oiiie, a primeira coisa que você vai precisar fazer aqui é tabelar essa função escrota, hahahha. Com sorte vc tem aquela calculadora que faz isso pra vc!!

Prontinho, tá tabelada a nossa função.

Passo 2

Agora bora começar a resolver as derivadas neh?!

A primeira coisa é lembrar que eu tenho 3 fórmulas possíveis pra achar a derivada, a forma avançada, atrasada ou central. Para o primeiro ponto da tabela, é obrigatório usar a avançada, pq não temos dados suficientes nem pra usar a central, nem para a atrasada.

f ' - 2.7 =   f - 2.7 + 0.2 - f ( - 2.7 ) 0.2

f ' - 2.7 =   0.11342 - 0.054797 0.2 = 0.293115

Agora, vamos utilizar para os próximos pontos a fórmula central, afinal ela erra menos neh?!

f ' - 2.5 = f - 2.5 + 0.2 - f ( - 2.5 - 0.2 ) 2 * 0.2

f ' - 2.5 = 0.65536 - 0.054797 2 * 0.2 = 1.5014

Para o próximo ponto também vamos usar a fórmula central.

f ' - 2.3 = f - 2.3 + 0.2 - f ( - 2.3 - 0.2 ) 2 * 0.2

f ' - 2.3 = 0.98472 - 0.11342 2 * 0.2 = 2.17825

Agora precisamos calcular a f ' ( - 2.1 ) , porém não temos dados suficientes (faltam pontos na tabela) para usar nem a fórmula central, nem a fórmula avançada. Então, utilizaremos a fórmula atrasada, blz?

f ' - 2.1 = f - 2.1 - f ( - 2.1 - 0.2 ) 0.2

f ' - 2.1 = 0.98472 - 0.65536 0.2 = 1.6468

Resposta

f ' ( - 2.7 ) = 0.2931

f ' ( - 2.5 ) = 1.5014

f ' ( - 2.3 ) = 2.17825

f ' ( - 2.1 ) = 1.6468

Exercícios de Livros Relacionados

27. Deduza a aproximação (2) para y ' ' ( x i ) usando a aproximação de y ( x ) por p 2 ( x ) conforme sugerido no texto.