Equação Segmentária da Reta

Fala Aí, nós somos o Responde Aí, e nossa missão é ajudar você a mandar bem na sua prova.

Quando estudamos matemática aprendemos que através de equações podemos desenhar no plano cartesiano retas, parábolas, círculos e muito mais. Falando em específico em relação as retas, conhecemos diversas maneiras de olhar para um equação que caracteriza uma reta, e hoje vamos conhecer mais uma.

Já conhecemos a "equação geral da reta" (), também a "equação fundamental da reta" () e a equação paramétrica da reta () e como será a equação segmentária da reta?

A equação segmentária da reta temo formato:

E pode ser rescrita como:

Onde:

• é coordenada em que a reta corta o eixo .
• é a coordenada em que a reta corta o eixo

Conforme a figura:

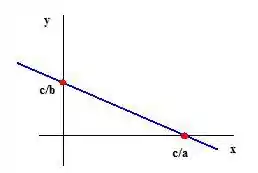
Então agora temos mais uma maneira de olhar para a equação da reta. Então a reta , pode ser reescrita como:

Dividindo por 6 dos dois lados:

Simplificando:

Graficamente:

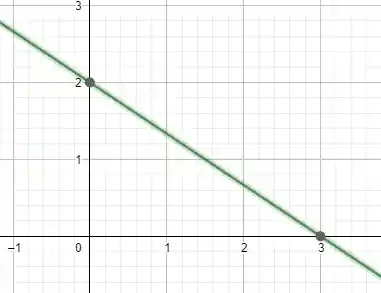
Tranquilo né? Confira o nosso site, para encontrar todo o conteúdo de Cálculo necessário para você seguir confiante nesse semestre temos exercícios resolvidos, conteúdo em vídeo, aulões e muito mais.