Equação da Circunferência
Resumo
A circunferência é a figura geométrica formada pontos que são equidistantes de um ponto fixo, chamado de centro. A distância entre o centro e cada ponto é chamada de
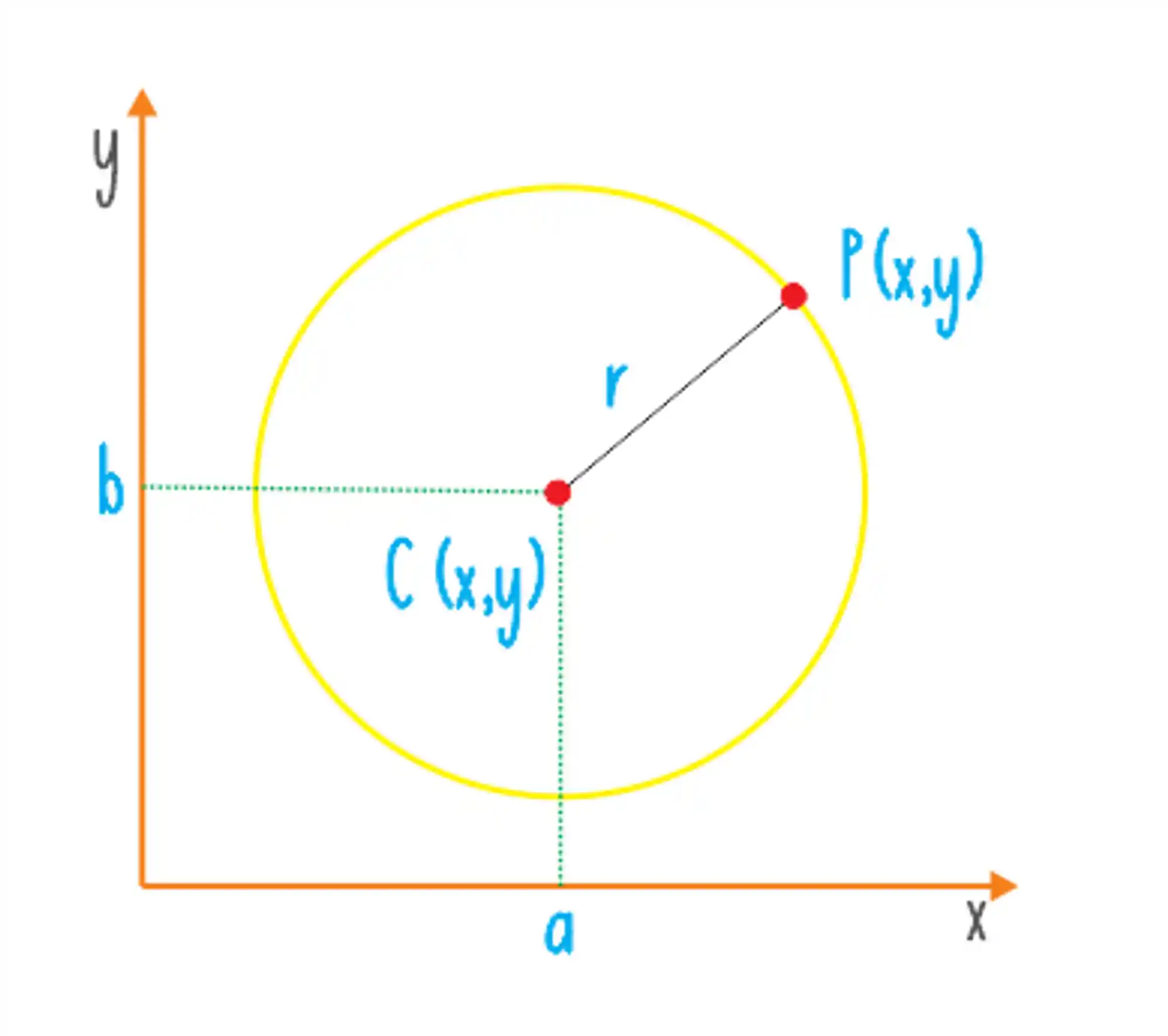
A Equação da Circunferência pode ser escrita como:
Onde:
e representam as coordenadas do ponto central da circunferência: e representam as coordenadas de um ponto qualquer da circunferência: representa o raio da circunferência, que pode ser calculado através da distância entre os pontos e
Exemplo: Determine a equação geral da circunferência de
Pra resolver esse problema usamos a equação da circunferência:
Substituindo os dados:
Abrindo a equação, ficamos com:
Dando aquela arrumadinha, temos:
Prontinho! Agora você pode dar uma conferida no nosso conteúdo sobre Curvas e Superfícies! Aqui no Responde Aí temos conteúdo em texto, vídeo, exercícios resolvidos passo a passo e mais!

Você também pode clicar aqui pra conferir a resolução de milhares de questões de livro! 🤩🤩🤩