Interseção de Superfícies: Parametrização
Produzido por Mariana PessanhaTeoria
Interseção de Superfícies
Quando duas curvas se interceptam, temos um (ou mais) ponto, certo? Agora, quando duas superfícies se interceptam, teremos uma curva.
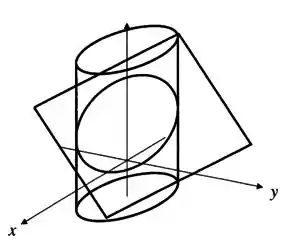
Se você fizer uma analogia, pode pensar o seguinte:
- Interseção de curvas (dimensão 1) são pontos (dimensão 0)
- Interseção de superfícies (dimensão 2) são curvas (dimensão 1)
Então vamos ver um exemplo de como encontrar essa curva de interseção. Considere o seguinte problema:
Encontre uma parametrização da curva formada pela interseção das seguintes superfícies:
Vamos seguir um passo a passo:
- Primeiro identificamos as equações das duas superfícies:
- Isolamos uma variável de umas das equações. Note que as duas superfícies são dois planos. Da segunda equação:
- Substituímos essa variável na outra equação. Vai ficar:
- E agora chegou a hora da parametrização. Podemos escolher a parametrização natural de :
- Por fim, substituimos essas parametrizações na terceira variável que foi isolada
Observação: Repara que essa é a projeção da curva no plano , pois a curva de interseção das duas superfícies está no espaço, mas chegamos a uma equação com apenas duas variáveis, já que isolamos o na primeira equação e depois substituímos nessa.
O mesmo acontece quando isolamos e : temos a projeção da curva no plano e ,respectivamente, pois nossa curva fica apenas em função das outras duas variáveis.
Logo:
Então a curva resultante da interseção dos dois planos pode ser expressa da seguinte forma:
Viu como é? Note que encontramos uma parametrização de uma reta, que é exatamente o que deveria ser a interseção de dois planos!
Bom, entendeu o espírito da coisa? Em geral, os procedimentos são os seguintes:
- Identificar as equações das duas superfícies
- Isolar uma variável de umas das equações
- Substituir essa variável na outra equação
- Parametrizar essa projeção da curva com as outras duas variáveis
- Substituir essas parametrizações na terceira variável que foi isolada
- Encontrar a parametrização da curva
Observação: sempre que uma das equações for um plano, execute o passo 2 isolando uma variável pela equação do plano!
Agora é colocar a mão na massa e manda brasa!