Exercícios de Parametrização da Interseção de Superfícies - Lista de Exercícios Resolvida

Encontre a parametrização da curva obtida pela interseção do hiperbolóide de uma folha e o plano .

Seja a superfície de equação

b1) Estude a intersecção de com cada plano e com o plano . Esboce .

b2) Encontre uma parametrização para a intersecção de com o plano .

Considere as superfícies

1. Exiba uma parametrização da curva espacial na forma

Explicitando , , , e .

Determine a parametrização da curva de interseção entre as duas superfícies abaixo.

Mostre que a projeção sobre o plano da curva de interseção das superfícies

É uma elipse.

Qual das superfícies seguintes não intercepta o plano vertical ?

(a)

(b)

(c)

(d)

(e)

A interseção das superfícies e é:

(a) uma parábola

(b) uma hipérbole

(c) uma elipse

(d) as superfícies não se interceptam

(e) uma circunferência

A interseção entre os planos

É (para ):

1. Uma reta, cuja equação paramétrica é
2. Uma reta, cuja equação paramétrica é
3. Uma reta, cuja equação paramétrica é
4. Uma reta, cuja equação paramétrica é
5. Uma reta, cuja equação paramétrica é

A imagem da curva , gerada por , está contida na interseção das superfícies

Suponha que e  .

1. Determine a reta tangente à curva no ponto ;
2. Determine uma curva nas condições acima.

Considere a curva como a interseção do plano , com o paraboloide . Uma parametrização da curva é:

a)

b)

c)

d)

e)

Uma parametrização da curva obtida pela interseção do semi-cone

Com o plano

É:

Seja a curva que é interseção das 2 superficies de equações

E

Então uma parametrização de , para é:

A interseção dos 2 planos de equações

E

É a reta parametrizada por:

Considere as superfícies descritas abaixo:

E estude as seguintes afirmações:

1. é vazia
2. �� vazia
3. é uma reta

Marque a alternativa correta

1. As afirmações I e II são falsas
2. As afirmações I e II são verdadeiras
3. As afirmações I e III são verdadeiras
4. Todas as afirmações são falsas
5. Todas as afirmações são verdadeiras

Uma parametrização da curva obtida como interseção do plano

Com a superfície definida por

É:

Considere as superfícies

E considere a superfície e a curva espacial .

a)Esboce a superfície e, sobre ela, desenhe a curva espacial .

b)Explicite uma parametrização da curva , determinando , e .

c) Seja a curva espacial obtida pela interseção da superfície com o plano , onde é a curva contida em e é a curva contida em .

1. Desenhe a curva espacial sobre a superfície
2. Identifique e como arcos de curvas planas conhecidas, denominando estas curvas e exibindo as suas equações cartesianas.
3. Encontre os pontos e de interseção das curvas e
4. Explicite as parametrizações de e , identificando os domínios destas.

Uma parametrização para a intersecção dos gráficos das funções e , em que , é dada por

em que , , e são número reais positivos.

Então, é igual a

a) .

b) .

c).

d) .

e) .

Encontre uma parametrização para curva dada pela intersecção do cilindro e do plano . Além disso, encontre as equações paramétricas da reta tangente à curva no ponto .

A curva parametrizada , obtida pela interseção do plano com o cilindro é dada por:

(a)

(b)

(c)

(d)

(e) nenhum dos outros itens

Considere uma curva dada pela interseção do cilindro com o plano . Uma parametrização de com , é:

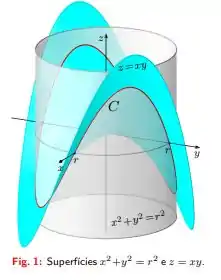
Seja a curva fechada dada pela interseção das superfícies de equações cartesianas e (Fig. 1).

Dê uma parametrização para a curva .

Considere as superfícies:

1. Determine uma parametrização para a curva de interseção ente as superfícies e .

Dê uma parametrização para a curva dada pela interseção das seguintes superfícies:

Dê uma parametrização para a curva dada pela interseção das seguintes superfícies:

Um arame tem a forma da interseção de

Calcule a massa do arame sabendo que sua densidade é dada por

Dê uma parametrização para a curva dada pela interseção das seguintes superfícies:

Dê uma parametrização para a curva dada pela interseção das seguintes superfícies:

Dê uma parametrização para a curva dada pela interseção das seguintes superfícies:

Dê uma parametrização para a curva dada pela interseção das seguintes superfícies:

Dê uma parametrização para a curva dada pela interseção das seguintes superfícies:

Calcule a massa da curva

sabendo que a densidade em cada ponto é inversamente proporcional ao quadrado da distância do ponto à origem.

Calcule

ao longo do eixo

Calcule

Uma parametrização para a intersecção dos gráficos das funções e , em que , é dada por

em que , , e são número reais positivos.

Então, é igual a

a) .

b) .

c).

d) .

e) .

Seja a quádrica cuja equação cartesiana é dada por .

Encontre uma parametrização para a curva que corresponde à interseção da quádrica com o plano .

e

Parametrize a curva de interseção de com .

Qual é um vetor diretor da reta que é a interseção dos planos e ?

(a)

(b)

(c)

(d)

(e)

Considere as superfícies

1. Explicite as coordenadas de vetores normais não-nulos e às superfícies e , respectivamente.
2. Exiba uma parametrização da curva espacial na forma

Explicitando , , , e .

Uma parametrização para a intersecção dos gráficos das funções e , em que , é dada por

em que , , e são número reais positivos.

Então, é igual a

a) .

b) .

c).

d) .

e) .

Uma parametrização para a intersecção dos gráficos das funções e , em que , é dada por

em que , , e são número reais positivos.

Então, é igual a

a) .

b) .

c).

d) .

e) .

A curva parametrizada por , , obtida pela interseção do plano e o cone é dada por:

a)

b)

c)

d)

e)

A interseção dos planos de equação e é a reta parametrizada por:

5. Nenhuma das alternativas anteriores.