Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Parametrização da Elipse

Ver Todos os Exercícios

Teoria

Fala aí! Bora aprender a fazer a Parametrização da elipse com o RespondeAí?!

Eu sei que esse nome assusta, mas não precisa ter medo! Parametrizar uma curva nada mais é do que pegar suas duas variáveis e escrever ela em função de apenas uma variável !

Hoje gente vai aprender como parametrizar uma elipse!

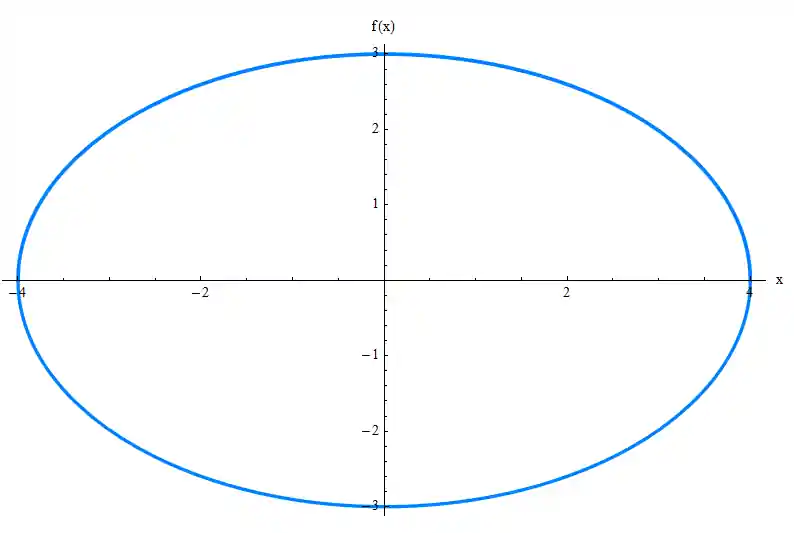
Elipse.
Elipse.

A elipse tem a seguinte forma geral:

Podemos escrever ela assim também:

Essa equação te lembra alguma coisa?!

Opaa! Segura essa informação que essa relação vai nos ajudar jajá!

Como Parametrizar uma Elipse?

Não precisa ficar com medo, é bem mais simples do que parece! Vamos aprender a fazer a parametrização da elipse colocando a mão na massa!

Com um exemplo:

A primeira coisa que precisamos fazer é escrever essa equação de um jeito que ela fique o mais parecida possível com a fórmula geral da elipse, podemos fazer então:

Ou melhor:

Lembra da nossa relação trigonométrica? Mas agora vamos escrever ela em função de :

Queremos escrever e em função de , então para isso fazemos:

Podemos isolar o e o ficamos então com:

Aweee! A Elipse esta parametrizada!

Agora só precisamos escrever o intervalo de , como temos uma volta completa, escrevemos:

De forma geral podemos dizer que a elipse do tipo:

Tem a seguinte parametrização:

Sacou?

Parametrizações Clássicas

Existem outras parametrizações de formas conhecidas, como a reta, circunferência, hipérbole, entre outras! Para aprender mais sobre parametrizações clássicas, confere esse vídeo que o RespondeAí preparou especialmente pra você 👇

Agora vamos praticar com exercícios?!

Como Parametrizar uma Elipse?

Parametrizações Clássicas

Exercícios Resolvidos

Exercício Resolvido #1

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p.12. questão 3.

Dê a parametrização para cada uma das curvas:

  1. A reta 2 x - 3 y = 6
  2. A parábola x 2 = 4 a y
  3. A circunferência x - a 2 + y - b 2 = r ²
  4. A elipse x 2 a 2 + y 2 b 2 = 1 ,   x ≥ 0
  5. O ramo da hipérbole x 2 a 2 - y 2 b 2 = 1 ,   x ≥ a
  6. A reta x - 1 2 = y + 1 3 = z - 1 2

Passo 1

a )

Para a reta 2 x - 3 y = 6 podemos isolar o y :

y = 2 3 x - 2

E usar a parametrização natural:

x t = t

y t = 2 3 t - 2

t ∈ R

Mas também podemos ver que os pontos 3,0 e 0 , - 2 pertencem a reta e o vetor diretor é n → = 3 - 0,0 - - 2 = ( 3,2 ) . Assim, essa reta também pode ser parametrizada como:

x t = 3 t

y t = 2 t - 2

t ∈ R

Passo 2

b )

Para a parábola x 2 = 4 a y também podemos isolar o y :

y = x 2 4 a

E usar a parametrização natural:

x t = t

y t = t 2 4 a

t ∈ R

Passo 3

c )

Para a circunferência x - a 2 + y - b 2 = r ² sabemos que a parametrização é:

x t = a + r cos ⁡ t

y t = b + r sen ⁡ t

t ∈ [ 0 ,   2 π ]

Passo 4

d )

Para a elipse x 2 a 2 + y 2 b 2 = 1 , sabemos que a parametrização é:

x t = a cos ⁡ t

y t = b sen ⁡ t

t ∈ [ - π 2 , π 2 ] pois x ≥ 0

Passo 5

e )

Para o ramo da hipérbole x 2 a 2 - y 2 b 2 = 1 ,   x ≥ a , sabemos que a parametrização da hipérbole é:

x t = acosh ⁡ t

y t = b s e n h t

t ∈ R

Passo 6

f )

Para a reta x - 1 2 = y + 1 3 = z - 1 2 , podemos fazer:

x - 1 2 = y + 1 3 = z - 1 2 = t

Assim:

x - 1 2 = t

y + 1 3 = t

z - 1 2 = t

Logo:

x t = 2 t + 1

y t = 3 t - 1

z t = 2 t + 1

A parametrização dessa reta é então:

x t = 2 t + 1

y t = 3 t - 1

z t = 2 t + 1

t ∈ R

Resposta

  1. x t = 3 t ,   y t = 2 t - 2 , t ∈ R
  2. x t = t , y t = t 2 4 a , t ∈ R
  3. x t = a + r cos ⁡ t , y t = b + r sen ⁡ t , t ∈ [ 0 ,   2 π ]
  4. x t = a cos ⁡ t , y t = b sen ⁡ t , t ∈ [ - π 2 , π 2 ]
  5. x t = acosh ⁡ t , y t = b s e n h t , t ∈ R
  6. x t = 2 t + 1 , y t = 3 t - 1   , z t = 2 t + 1 , t ∈ R

Exercício Resolvido #2

Elaboração Própria

1 – Encontre uma parametrização para os seguintes círculos com centro em C 0 e raio r :

  1. C 0 = ( 1 , - 1 ) e r = 2
  2. C 0 = ( 1 ,   3 ) e r = 3

2 – Encontre uma parametrização para as seguintes curvas:

  1. x - 2 2 + y - 1 2 = 4
  2. 2 x 2 + y 2 = 1
  3. 9 x 2 + 4 y 2 + 18 x - 16 y = 11

Passo 1

a:

Temos que

x 0 = 1   y 0 = - 1   r = 2

Substituindo nas equações paramétricas:

x t = x 0 + r cos ⁡ t = 1 + 2 cos ⁡ t

y t = y 0 + r sen ⁡ t = - 1 + 2 sen ⁡ t

⇒ σ t = ( 1 + 2 cos ⁡ t ,   - 1 + 2 sen ⁡ t )

t ∈ 0 ,   2 π

Passo 2

Item 1, (b):

Temos que

x 0 = 1   y 0 = 3   r = 3

Substituindo nas equações paramétricas:

x t = x 0 + r cos ⁡ t = 1 + 3 cos ⁡ t

y t = y 0 + r sen ⁡ t = 3 + 3 sen  ⁡ t

⇒ σ t = ( 1 + 3 cos ⁡ t ,   3 + 3 sen ⁡ t )

t ∈ 0 ,   2 π

Passo 3

Item 2, (a):

Essa é a equação de um círculo de centro ( 2 ,   1 ) e raio   r = 2 :

x - 2 2 + y - 1 2 = 4

Logo:

x ( t ) = 2 + 2 cos ⁡ t

y ( t ) = 1 + 2 sen ⁡ t

⇒ σ t = ( 2 + 2 cos ⁡ t ,   1 + 2 sen ⁡ t )

t ∈ [ 0 ,   2 π ]

Passo 4

Item 2, (b):

Essa é a equação de uma elipse:

2 x 2 + y 2 = 1

Colocando na forma x - x 0 2 a 2 + y - y 0 2 b 2 = 1 :

x 2 1 2 + y 2 = 1

Logo:

x 0 = 0 y 0 = 0 a 2 = 1 2 ⇒ a = 2 2 b 2 = 1 ⇒ b = 1

Substituindo na parametrização:

x t = x 0 + a cos ⁡ t = 0 + 2 2 cos ⁡ t = 2 2 cos ⁡ t

y t = y 0 + b sen ⁡ t = 0 + 1 sen ⁡ t = sen ⁡ t

⇒ σ t = 2 2 cos ⁡ t ,   sen ⁡ t

t ∈ [ 0 ,   2 π ]

Passo 5

Item 2, (c):

9 x 2 + 4 y 2 + 18 x - 16 y = 11

⇒ 9 x 2 + 18 x + 4 y 2 - 16 y = 11

Quando houver termos ao quadrado ( x 2 ) misturados com termos lineares ( x ), completamos quadrados.

O procedimento é esse:

  1. Some um termo b 2
  2. Iguale com o quadrado a 2 + 2 a b + b 2
  3. Compare termo a termo
  4. Encontre a e b
  5. Substitua e fatore: a + b 2

Vamos completar esse quadrado:

9 x 2 + 18 x

  1. Somar um termo b 2 :

    2. 9 x 2 + 18 x + b 2

  2. Igualar com o quadrado   a 2 + 2 a b + b 2 :

    3. 9 x 2 + 18 x + b 2 = a 2 + 2 a b + b 2

  3. Comparar termo a termo:

    4. 9 x 2 = a 2 18 x = 2 a b b 2 = b 2

  4. Encontrar a e b :

    5. Pela primeira equação, vemos que a = 3 x . Substituindo na segunda, encontramos b = 3 . Logo:

    a = 3 x b = 3

  5. Substituir e fatorar:

Agora é só substituir o termo b 2 na expressão:

9 x 2 + 18 x + b 2 = 9 x 2 + 18 x + 9

E essa expressão pode ser fatorada como a + b 2 :

Como já conhecemos a e b , basta substituir:

9 x 2 + 18 x + 9 = 3 x + 3 2

Vamos agora completar o outro quadrado:

4 y 2 - 16 y

  1. Somar um termo b 2 :

    2. 4 y 2 - 16 y + b 2

  2. Igualar com o quadrado a 2 + 2 a b + b 2 :

    3. 4 y 2 - 16 y + b 2 = a 2 + 2 a b + b 2

  3. Comparar termo a termo:

    4. 4 y 2 = a 2 - 16 y = 2 a b b 2 = b 2

  4. Encontrar a e b :

    5. Pela primeira equação, vemos que a = 2 y . Substituindo na segunda, encontramos b = 3 . Logo:

    a = 2 y b = - 4

  5. Substituir e fatorar:

Agora é só substituir o termo b 2 na expressão:

4 y 2 - 16 y + b 2 = 4 y 2 - 16 y + 16

E essa expressão pode ser fatorada como   a + b 2 . Como já conhecemos a e b , basta substituir:

4 y 2 - 16 y + 16 = 2 y - 4 2

Agora vamos substituir na equação original:

9 x 2 + 18 x + 4 y 2 - 16 y = 11

9 x 2 + 18 x + 9 ⏟ 3 x + 3 2 + 4 y 2 - 16 y + 16 ⏟ 2 y - 4 2 = 11 + 9 + 16

⇒ 3 x + 3 2 + 2 y - 4 2 = 36

⇒ 3 2 x + 1 2 + 2 2 y - 2 2 = 36

⇒ 9 x + 1 2 + 4 y - 2 2 = 36

Dividindo por 36 os dois lados:

⇒ 9 36 x + 1 2 + 4 36 y - 2 2 = 36 36

⇒ x + 1 2 4 + y - 2 2 9 = 1

Pronto! Chegamos à equação da elipse. Comparando com a equação x - x 0 2 a 2 + y - y 0 2 b 2 = 1 :

x 0 = - 1 y 0 = 2 a 2 = 4 ⇒ a = 2 b 2 = 9 ⇒ b = 3

Logo, a parametrização fica assim:

x t = x 0 + a cos ⁡ t = - 1 + 2 cos ⁡ t

y t = y 0 + b sen ⁡ t = 2 + 3 sen ⁡ t

⇒ σ t = ( - 1 + 2 cos ⁡ t ,   2 + 3 sen ⁡ t )

t ∈ [ 0 ,   2 π ]

Resposta

    1. σ t = ( 1 + 2 cos ⁡ t ,   - 1 + 2 sen ⁡ t )

      t ∈ 0 ,   2 π

    σ t = ( 1 + 3 cos ⁡ t ,   3 + 3 sen ⁡ t )

    t ∈ 0 ,   2 π

  1. σ t = ( 2 + 2 cos ⁡ t ,   1 + 2 sen ⁡ t )

    t ∈ [ 0 ,   2 π ]

  2. σ t = 2 2 cos ⁡ t ,   sen ⁡ t

    t ∈ [ 0 ,   2 π ]

σ t = ( - 1 + 2 cos ⁡ t ,   2 + 3 sen ⁡ t )

t ∈ [ 0 ,   2 π ]

Exercício Resolvido #3

Elaboração própria

Uma partícula se move a partir do ponto 1 ,   6 em cima da circunferência x 2 - 2 x + y 2 = 5 . Ela dá uma volta no sentido anti-horário, e depois duas no sentido horário. Parametrize a trajetória dessa partícula.

Passo 1

Vamos parametrizar a circunferência, completando quadrados:

x - 1 2 - 1 + y 2 = 5

x - 1 2 + y 2 = 6

Então temos

x = 6 cos ⁡ t + 1 y = 6 sen ⁡ t

Passo 2

Agora vamos identificar em que tempo t 0 a partícula inicia sua trajetória. Temos

x t 0 ,   y t 0 = 1 , 6

6 cos ⁡ t 0 + 1 ,   6 sen ⁡ t = 1 ,   6

Então

cos ⁡ t 0 = 0 sen ⁡ t 0 = 1 ⇒ t 0 = π 2

Passo 3

Agora vejamos em que intervalo varia o parâmetro t .

A trajetória tem duas partes: na primeira a partícula dá uma volta (rotação de 2 π = 4 π 2 ), e na segunda ela dá duas voltas (rotação de 4 π = 8 π 2 ). E começamos em t 0 = π 2 . Logo:

  • 1ª parte da trajetória: t ∈ π 2 , 5 π 2
  • 2ª parte da trajetória: t ∈ 5 π 2 , 13 π 2

Passo 4

Agora temos que ver a questão do sentido de rotação. A 1ª parte se faz no sentido anti-horário, então mantemos o sinal positivo.

Agora, vamos analisar a segunda parte. No instante t = 5 π 2 , quando a partícula começa a se mover no sentido horário, ela se encontra no ponto 1 , 6 . Veja a figura abaixo.

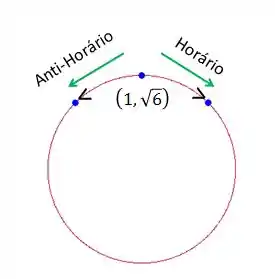
Perceba que, nesse caso, tanto o deslocamento no sentido horário quanto no sentido anti-horário terão em comum a coordenada y . Ou seja, não iremos mudar a coordenada y da parametrização.

Porém, elas diferem na coordenada x . Se a partícula continuasse no sentido anti-horário, estaria indo na direção negativa do eixo x , porém no sentido horário ela estaria indo na direção positiva do eixo x . Logo, vamos inverter o sinal do cosseno na parametrização.

Então a parametrização da trajetória da partícula é:

x = 6 cos ⁡ t + 1 y = 6 sen ⁡ t ,   t ∈ π 2 , 5 π 2

x = - 6 cos ⁡ t + 1 y = 6 sen ⁡ t ,   t ∈ 5 π 2 , 13 π 2

Lembrando de não mexer no sinal do + 1 ali!! Só trocamos o sinal do cosseno e do seno!

Resposta

x = 6 cos ⁡ t + 1 y = 6 sen ⁡ t ,   t ∈ π 2 , 5 π 2

x = - 6 cos ⁡ t + 1 y = 6 sen ⁡ t ,   t ∈ 5 π 2 , 13 π 2

Exercícios de Livros Relacionados

Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.d) r → t = 2 cos 3 ⁡ t ,2 s e n 3 t , t ∈ 0 , π 2
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.b) r → t = t ,t + 2 ,4 - 2 t , t ∈ 0 ,1
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.a) r → t = 2 + 3 cos ⁡ t ,1 + 4 s e n t , t ∈ 0 ,2 π