Teoria
A Regra da Cadeia é uma propriedade de derivação que vai ser muito utilizada por você nos seus exercícios e provas!
Quer que eu te prove?! Então deriva essa função pra mim:
-Como eu faço isso?! 😱😱😱😱
Para isso você vai usar a Regra da Cadeia! 😍😍😍
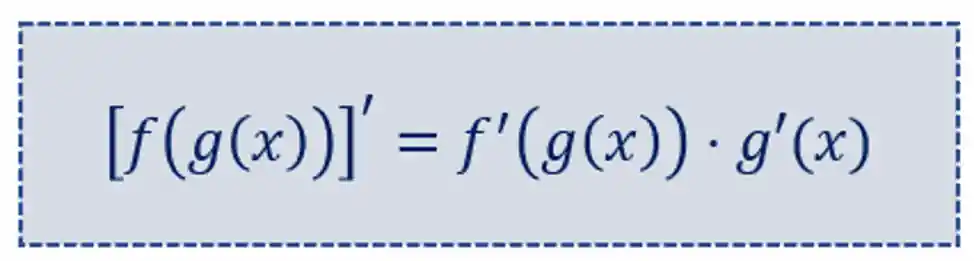
Carinha esquisita, não é?! Mas não se preocupa!
Fica comigo que no final eu vou te ensinar a derivar essa função cabulosa ai de cima! Mas primeiro vamos aprender o que é a regra da cadeia e como usa-lá! Se liga nesse videozinho aqui: 👇
Ou continua comigo no textinho! 😁
Quando Usar a Regra da Cadeia?
A Regra da Cadeia vai ser utilizada sempre que tivermos uma função composta, que nada mais é do que uma função dentro de outra, ou seja um "aninhamento" de funções!
Por exemplo:
Nesse caso podemos dizer que:
-Beleza, mas como fazer a Regra da Cadeia?
A primeira parte é identificar, dentro da função principal,
A primeira é um polinômio:
A segunda é uma função exponencial:
- Clique para saber mais:
Agora só aplicamos a fórmula da regra da cadeia:
Fica assim:
E essa é a nossa resposta! Simples assim 😁
Mas essa foi fácil! Agora vamos ver um passo a passo mais detalhado com um outro exemplo?!
Regra da Cadeia: Passo a Passo
Então sem perda de tempo, vamos ver como resolvemos derivadas utilizando a Regra da Cadeia!
- Derive a equação:
Passo 1
Nesse exercício, primeiro vamos identificar as funções que compõe a função
Então fazemos:
Já conseguimos separar nossas funções.
Passo 2
Então agora podemos dizer que
A derivada de quem está fora:
A derivada de quem está dentro:
Vamos aplicar a regra da cadeia.
Passo 3
A Regra da Cadeia diz para gente que a nossa derivada, é a derivada de quem está fora repetindo quem está dentro, vezes a derivada de quem está dentro, então no caso do exemplo teríamos:
Não esquece de colocar o termo
Resposta
Agora vamos finalmente resolver o exemplo do início!
Resolução:
- Derive a função:
Acompanhe a resolução em vídeo que o RespondeAí preparou especialmente pra você: 👇
Vamos praticar com mais exercícios?
Quando Usar a Regra da Cadeia?
Regra da Cadeia: Passo a Passo
Resolução:
Exercícios Resolvidos
Exercício Resolvido #1
UFF, Cálculo IA-Lista 6, GMA, 2008-1, Questão 10.
Derive a seguinte função (se possível, simplifique a função e/ou a derivada da função).
Passo 1
Neste caso é como se tivéssemos uma função “dentro” da outra. A função estaria dentro da função , deste modo:
Agora, a gente consegue separar a função em duas. Então vamos chamar a função cosseno de e a função de , ficando assim,
Como, a função cosseno está dentro da função . Teremos,
Passo 2
A gente tem pela Regra da Cadeia que, para uma qualquer, temos sua derivada dada por:
O que isso que dizer? Nós vamos primeiro derivar a função de fora e multiplicar pela derivada da função de dentro.
Derivando a função de fora ficamos com,
Derivando a função de dentro ficamos com,
Passo 3
Agora substituímos na fórmula da derivada pela Regra da Cadeia:
Essa é a derivada!
Resposta
Exercício Resolvido #2
George B. Thomas Jr., Cálculo volume I, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp.199-78b
Determine usando a regra da cadeia, sendo uma função composta de
Passo 1
Ora, nesse caso nós temos um em função de e um em função de . Assim podemos escrever:
Passo 2
Para derivar esse cara, usamos a Regra da Cadeia:
Escrevendo de outra forma, nós temos,
Passo 3
Derivando cada uma das funções que mostramos na Regra da Cadeia, ou seja, e , teríamos:
Logo, substituindo as derivadas na expressão da Regra da Cadeia :
Passo 4
Novamente, nós temos um em função de e um em função de . Assim, é possível escrever:
Passo 5
Para derivar esse cara, usamos a Regra da Cadeia:
Escrevendo de outra forma, nós temos,
Passo 6
Derivando cada uma das funções, teríamos:
Logo, substituindo as derivadas na expressão da Regra da Cadeia:
Resposta
Exercício Resolvido #3
Elaboração própria
Derive a função:
Passo 1
Tem duas formas de fazer essa derivada, uma mais direta ao ponto e outra usando fórmulas. Fica a seu gosto qual você prefere, beleza? Mas relaxa que vamos ver as duas.
Vou, antes de tudo, dar uma desmembrada na função. Repara comigo, é como se ali estivessem escritas duas funções, observadas de fora pra dentro:
De modo que uma estaria dentro da outra, desta forma:
Reparou? Isso cai na Regra da Cadeia.
Passo 2
Vamos derivar então. Seguindo a regra da cadeia:
Isso vai dar:
No caso, eu vou ter que repetir essa Regra mais uma vez. Porque repara bem, é como se tivéssemos de novo uma função dentro da outra:
Fazendo a regra da cadeia de novo:
E cara, ainda não acabou! Vamos precisar aplicar a regra da cadeia mais uma vez (virou um combo isso aí rs)! Isso porque podemos enxergar a derivada que sobrou como:
E fazendo a regra da cadeia temos:
Passo 3
Agora chegamos na parte boa em que fechamos a questão, juntando tudo que vimos:
Chegamos à:
Passo 4
A outra forma da gente resolver é identificar logo todas as funções que estão dentro uma da outra. Aí acabamos montando uma fórmula bem grande. Veja bem:
Pode ser entendido como:
Se fizermos:
Como pra fazer regra da cadeia três vezes vamos precisar de todas as derivadas, temos:
Então mãos a obra, derivando uma primeira vez:
E não tem jeito, o carinha lá do final também vai ser derivado usando a regra da cadeia:
E uma terceira e última vez também tem que ser feita:
De forma que a derivada vai ficar:
Agora é só substituir já que sabemos todas as funções e suas derivadas. Pro primeiro termo dos quatro, temos com substituído por , logo:
No segundo termo, temos com substituído por , logo:
No terceiro termo, temos com substituído por , logo:
E pra finalizar sobrou só o já conhecido. Juntando tudo:
A derivada fica:
Eu sei, a questão foi meio grandinha. Mas confia: é tudo questão de ter a definição da Regra da Cadeia e as derivadas das funções importantes memorizadas e atenção na hora disso tudo. Com o tempo vem a prática, e você vai derivar tudo de olho fechado. ;)
Resposta
Exercício Resolvido #4
Derive:
Passo 1
Quando a gente olha pra uma função elevada a uma função já dá um nó na cabeça, não é mesmo? Parece difícil a beça e já da um medo! Mas calma, tem uma propriedade das exponenciais que salva muito a gente nesses casos, dá uma olhada:
Sendo um número qualquer. Ok, mas se ao invés de tivéssemos uma função?
Nada de diferente pessoal! Nada mesmo! Então vamos usar essa propriedade e escrever:
E, pra fechar esse passo, vamos usar mais uma propriedade importante, dessa vez dos logaritmos:
E se você acha que isso vale também pra funções, achou certo! Vamos ter então:
Opa, agora talvez fique mais tranquilo da gente derivar! Vamo que vamo então:
Passo 2
Se lembrarmos bem, quando derivamos elevado a alguma função, pela regra da cadeia, ficamos com:
Olhando bem pra nossa função e comparando com a regra da cadeia em cima
A gente vê bem que é esse . No caso, vai ser:
Bem, vai faltar só derivar agora! E a derivada dessa função então vai ser, pela regra do produto:
Passo 3
Fechamos a questão então galera! Próximo passo é só juntar tudo que encontramos, que foi:
Juntando tudo:
E lá do primeiro passo, pescando essa informação importantíssima:
Fechamos a questão com:
Resposta
Exercício Resolvido #5
PUC-RJ - Cálculo 1 - P4 2010.1 - 1 b
Derive as funções abaixo:
Passo 1
Temos aqui uma função composta. Há uma por fora, e uma função dentro dela dada por . Por definição, derivamos pela Regra da Cadeia a e ficaríamos assim:
Passo 2
Vamos determinar e
Passo 3
Para determinar a derivada de precisamos recorrer a regra da cadeia de novo, onde
Passo 4
Agora vamos na fórmula que achamos para a Derivada de :
Resposta
Exercício Resolvido #6
James Stewart, Cálculo Vol.1, 5ª ed. São Paulo: Pioneira Thomson Learning, 2006, Pg 224, exercício 53
Suponha que e , g’(3)=4 , e . Enconte
Passo 1
Eita! Essa questão tá pedindo pra gente a derivada, mas nem disse qual é a função? E agora o que a gente faz? Então ele nos fala que é uma função composta e nos dá alguns pontos e suas derivadas em determinados pontos para encontrarmos .
Portanto queremos encontrar:
Em x=3
Passo 2
Vamos então substituir e na expressão anterior
Caímos numa nova incógnita agora , mas essa informação nos foi dada no enunciado, então é só substituir e encontramos a resposta.
Passo 3
Substituindo agora
Resposta
Exercício Resolvido #7
James Stewart, Cálculo Vol. 1, 5ª ed. São Paulo: Pioneira Thomson Learning, 2006, Pg 241, exercício 59 -modificada
Encontre em termos de , e . Onde
Passo 1
Bem, aqui ele quer a segunda derivada daquela função , isso porque tem aquelas duas linhas em cima da .
Para achar essa segunda derivada temos que derivar duas vezes, lembra? Vamos derivar então.
Repara que dentro da na equação da , temos um isso nos diz que temos que usar a regra da cadeia, vamos fazer
Isso vai ajudar nas nossas contas para entender qual função está dentro da onde e como fica a regra da cadeia. A nossa vai ficar
Passo 2
Fazendo a primeira derivada vamos ter que aplicar a regra da cadeia e a regra do produto, então vamos ter
Então vamos ter
Passo 3
Vamos trocar só a derivada de ali em cima, isso porque vai ajudar nas contas, como temos que derivar de novo para achar a segunda derivada vamos deixar o dentro da e da
Assim a vai ficar
Passo 4
Vamos, agora, para a segunda derivada. Vamos usar, de novo, a regra do produto e a regra da cadeia.
Agora, trocando a derivada de que já calculamos ali em cima vamos ter
Agora podemos trocar por , afinal a nossa resposta só pode depender de , , e .
Resposta
Exercício Resolvido #8
Elaboração Própria
Seja uma função diferenciável tal que e . Considere a função
Calcule .
Passo 1
Vamos calcular . Começando com a regra do produto:
Passo 2
Agora temos que mandar uma regra da cadeia pra achar a derivada dessa parte da direita:
Pelas regras da cadeia e do quociente, temos que
Ou seja,
Passo 3
Juntando isso tudo:
Passo 4
Beleza, agora podemos achar ! Repare que substituindo , temos .
Então temos
E pelo enunciado, . Ele também deu , ou seja:
É isso!