Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Derivada Implícita

Ver Todos os Exercícios

Teoria

Fala aí! Seja muito bem vindo ao Responde Aí! Bora entender o que é uma Derivada Implícita na prática?!

Pra começar com tudo eu vou te desafiar a calcular a derivada da função a baixo com relação a :

-Beleza, eu tenho que isolar o , mas como?! 😱

É pra problemas assim que a gente usa a derivação implícita! 🤩 Se liga nesse videozinho abaixo que vai te ensinar tudo o que você precisa saber! 👇

Ou segue comigo no textinho! 👇

Como Calcular a Derivada Implícita?

Pra aprendermos a fazer a derivação implícita vamos usar o exemplo lá de cima:

Passo 1: Escrever a Derivada dos Dois Lados

Escrevemos assim:

Como a derivada de uma constante é igual a zero, já podemos simplificar o lado direito da expressão:

Passo 2: Dividir a Derivada em Partes

Nesse exemplo temos um polinômio, como a derivada da soma é a soma das derivadas, podemos fazer:

A primeira derivada a gente já pode calcular:

Ficamos com:

Passo 3: Derivação Implícita

Agora que vem o pulo do gato!

-Como podemos derivar e em função de ?

Usamos a regra da cadeia! Ou, simplificando, você deriva em função de e depois multiplica pela derivada de , que é :

Dessa forma ficamos com:

Agora só precisamos isolar o e simplificar a expressão:

Prontinho! Calculamos a derivada implícita!

Agora vamos praticar com exercícios?!

Como Calcular a Derivada Implícita?

Exercícios Resolvidos

Exercício Resolvido #1

George B. Thomas Jr., Cálculo volume I, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp.209-37

No exercício, use a derivada implícita para determinar d y / d x .

x 2 + y 2 = 1

Passo 1

Vamos derivar os dois lados em função de x :

x 2 ' + y 2 ' = 1 '

Nesse momento, calculamos todas as derivadas em função de x diretamente e as derivadas em função de y nós derivamos para y adicionando, no fim, um y ' :

2 x + 2 y y ' = 0

2 x + 2 y y ' = 0

Passo 2

Agora é só evidenciar o y ' :

2 y y ' = - 2 x

y ' = - 2 x 2 y = - x y

Resposta

d y d x = - x y

Exercício Resolvido #2

George B. Thomas Jr., Cálculo volume I, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp.209-44

Se x y + y 2 = 1 , encontre o valor de d y / d x no ponto 0 , - 1 .

Passo 1

Vamos derivar os dois lados em função de x :

x y ' + y 2 ' = 1 '

Aplicamos a Regra do Produto no primeiro cara

x ' y + x y ' + y 2 ' = 1 '

Passo 2

Nesse momento, calculamos todas as derivadas em função de x diretamente e as derivadas em função de y nós derivamos para y adicionando, no fim, um y ' :

1 y + x y ' + 2 y y ' = 0

y + x y ' + 2 y y ' = 0

Passo 3

Agora é só evidenciar o y ' :

y + y ' x + 2 y = 0

y ' x + 2 y = - y

y ' = - y x + 2 y

Passo 4

Usando x , y = 0 , - 1 teremos:

y ' = - - 1 0 + 2 - 1

= - - 1 - 2 = - 1 2

Resposta

d y d x 0 , - 1 = - 1 2

Exercício Resolvido #3

Elaboração Própria

Encontre a derivada y ' no ponto P = 1 , 1 + 5 2 da curva definida implicitamente abaixo:

x 3 + x y - y 2 = 0

Passo 1

Derivando em ambos os lados, obtemos:

3 x 2 + x ' y + x y ' - y 2 ' = 0

Passo 2

Aplicando a regra da cadeia, teremos

y 2 = 2 y y '

Assim,

3 x 2 + y + x y ' - 2 y y ' = 0

3 x 2 + y + x y ' - 2 y y ' = 0

Passo 3

Isolando a variável y ' :

y ' x - 2 y = - y - 3 x 2

y ' = - y - 3 x 2 x - 2 y

Passo 4

Substituindo os valores:

P = 1 , 1 + 5 2

y ' 1 , 1 + 5 2 = - 1 + 5 2 - 3 × 1 2 1 - 2 × 1 + 5 2

y ' 1 , 1 + 5 2 = - 1 - 5 2 - 3 1 - 1 + 5

y ' 1 , 1 + 5 2 = - 1 - 5 - 6 2 1 - 1 - 5

O que, continuando as contas, resulta em:

y ' 1 , 1 + 5 2 = - 7 - 5 2 - 5 = - 7 - 5 - 2 5 = 7 + 5 2 5 = 7 5 + 5 10

y ' 1 , 1 + 5 2 = 5 + 7 5 10

Resposta

y ' 1 , 1 + 5 2 = 5 + 7 5 10

Exercício Resolvido #4

Elaboração própria

Encontre d y d x no ponto ( 1,1 ) diferenciando implicitamente a curva definida por

x y = 2 x 3 y 2 - 1

Passo 1

Bom, ele pediu a derivada de y em relação a x . Para isso ele pede que a gente faça derivação implícita. Lembra que a derivação se caracteriza por adicionar um y ' (pela Regra da Cadeia) na derivação, que é justamente quem a gente procura, no ponto ( 1,1 ) .

x y ' = 2 x 3 y 2 - 1 '

Passo 2

Para o primeiro termo, temos que derivar a raiz e depois adicionar, pela Regra da Cadeia, a derivada do que está dentro dela:

x y ' = 1 2 1 x y x y '

Passo 3

Para o termo da derivada ali em cima, usamos a Regra do Produto, lembrando que y é derivada de forma implícita:

1 2 1 x y x y ' = 1 2 1 x y 1 y + x y ' = 1 2 1 x y y + x y '

Passo 4

Para o segundo termo basta derivar direto, usando a Regra do Produto no segundo termo:

2 x 3 y 2 - 1 ' = 2 3 x 2 y 2 + 2 x 3 2 y y ' + 0 = 6 x 2 y 2 + 4 x 3 y y '

Passo 5

Juntando tudo:

x y ' = 2 x 3 y 2 - 1 '

1 2 x y y + x y ' = 6 x 2 y 2 + 4 x 3 y y '

Substituindo x ,   y por ( 1,1 ) :

1 2 ( 1 ) ( 1 ) ( 1 ) + ( 1 ) y ' = 6 1 2 1 2 + 4 1 3 1 y '

1 2 1 + y ' = 6 + 4 y '

1 2 + y ' 2 = 6 + 4 y '

Multiplicando tudo por 2:

1 + y ' = 12 + 8 y '

⇒ 7 y ' = - 11

y ' = - 11 7

Resposta

y ' = d y d x = - 11 7

Exercício Resolvido #5

George B. Thomas Jr., Cálculo volume I, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp 209 – 62

O fólio de Descartes

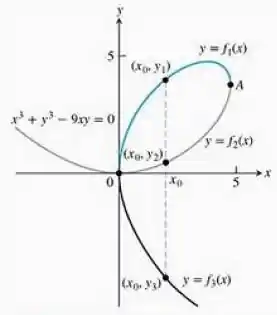
a Encontre o coeficiente angular do fólio de Descartes, x 3 + y 3 - 9 x y = 0 nos pontos 4,2 e 2,4

b Em qual ponto, além da origem, o fólio tem uma tangente horizontal?

c Encontre as coordenadas do ponto A da figura, onde o fólio tem uma tangente vertical.

Passo 1

a O cara nos pediu o coeficiente angular,   a . O que eu te contei na teoria? O coeficiente angular é a derivada da função avaliada nos pontos que ele nos deu. Então vamos precisar derivar a expressão do fólio.

Passo 2

Vamos achar a derivada y ' por Derivação Implícita:

x 3 + y 3 - 9 x y ' = 0 '

x 3 ' + y 3 ' - 9 x y ' = 0

Observa que para o termo 9 x y , vamos precisar usar a regra do produto

3 x 2 + 3 y 2 y ' - 9 x ' y - 9 x y ' = 0

3 x 2 + 3 y 2 y ' - 9 y - 9 x y ' = 0

y ' 3 y 2 - 9 x = 9 y - 3 x 2

y ' = 9 y - 3 x 2 3 y 2 - 9 x

Passo 3

Aplicando os pontos, ficamos com:

y ' 4,2 = 9 2 - 3 4 2 3 2 2 - 9 4 = 18 - 48 12 - 36

= - 30 - 24 = 5 4

y ' 2,4 = 9 4 - 3 2 2 3 4 2 - 9 2 = 36 - 12 48 - 18

= 24 30 = 4 5

Passo 4

b Ele pede que achemos o ponto onde a tangente é horizontal.

Ora, uma reta horizontal tem inclinação zero, ou seja, seu coeficiente angular é nulo. Portanto, o que queremos achar é:

y ' = 9 y - 3 x 2 3 y 2 - 9 x = 0

9 y - 3 x 2 = 0

y = x 2 3

Ou seja, todos os pontos que satisfazem essa igualdade vão zerar a derivada.

Passo 5

Para encontrar o ponto que vem dessa igualdade, jogamos ela na equação da curva:

x 3 + y 3 - 9 x y = 0

x 3 + x 6 27 - 9 x x 2 3 = 0

x 3 + x 6 27 - 3 x 3 = 0

x 6 27 - 2 x 3 = 0

Multiplicando tudo por 27

x 6 - 54 x 3 = 0

x 6 - 54 x 3 = 0

x 3 x 3 - 54 = 0

Como ele pede para desconsiderar o ponto da origem, a solução x 3 = 0 não nos interessa.

x 3 = 54 → x = 3 2 3

Passo 6

O y para esse valor de x vai ser:

y = x 2 3

y = 3 2 3 2 3

y = 3 4 3

O ponto será, portanto:

3 2 3 , 3 4 3

Passo 7

c Ele pede que achemos uma tangente vertical agora.

Ora, uma reta vertical tem inclinação “infinita”, ou seja, seu coeficiente angular é explode para ± ∞ . Portanto, o que queremos achar é:

y ' = 9 y - 3 x 2 3 y 2 - 9 x = ± ∞

Isso acontecerá quando o denominador zerar sem que haja indeterminação 0 0 . Ou seja, queremos que

3 y 2 - 9 x = 0

x = y 2 3

Para encontrar o ponto que vem dessa igualdade, jogamos ela no termo inicial:

x 3 + y 3 - 9 x y = 0

y 6 27 + y 3 - 9 y y 2 3 = 0

y 6 - 54 y 3 = 0

y 3 y 3 - 54 = 0

Passo 8

Como ele pede para desconsiderar o ponto da origem, a solução y 3 = 0 não nos interessa.

y 3 = 54 → y = 3 2 3

O x para esse valor de y vai ser:

x = y 2 3

x = 3 2 3 2 3

x = 3 4 3

O ponto A será, portanto:

3 4 3 , 3 2 3

Resposta

a   y ' 4,2 = 5 4

y ' 2,4 = 4 5

b   3 2 3 , 3 4 3

c   A = 3 4 3 , 3 2 3

Exercícios de Livros Relacionados

Nos Exercicios de 1 a 28, ache d y d x por derivação implícita7. x + y = 4
Exercício de Livro
Encontre d y // d x derivando implicitamente.x^2 + y^3 = 1
Considere y como variável independente e x como variável dependente e use a derivação implícita para encontrar d x / d y . y sec ⁡ x = xt gy
a) Encontre y ' derivando implicitamente.b) Resolva a equação explicitamente isolando y e derive para obter y ' em função de x .c) Verifique que sua soluções das partes (a) e (b) são consistentes, sub