Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Regra do Produto e do Quociente

Ver Todos os Exercícios

Teoria

Hoje a gente vai aprender duas regras de derivação super importantes. A Regra do Produto e a Regra do Quociente! Bora lá?!

Regra do Produto

O que você faria se eu te pedisse pra derivar essa função aqui:

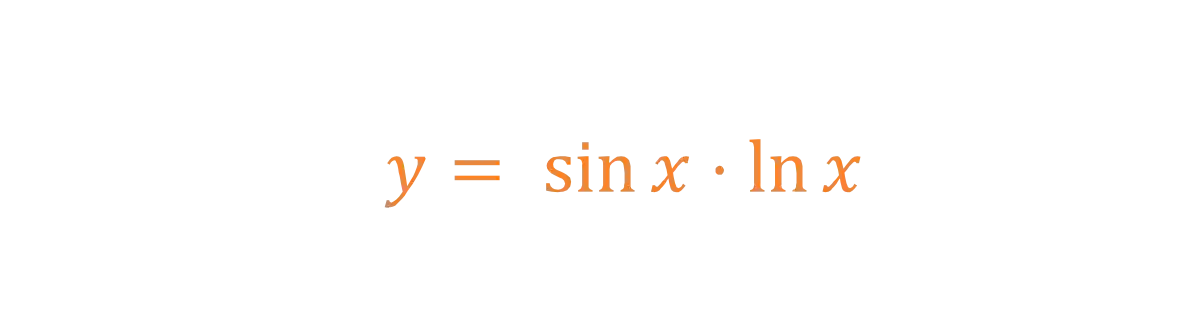
Produto de duas funções
Produto de duas funções

Como podemos ver, é uma função composta por duas outras funções e . Pra resolver esse tipo de problema usamos a Regra do Produto!

Ela tem essa carinha aqui:

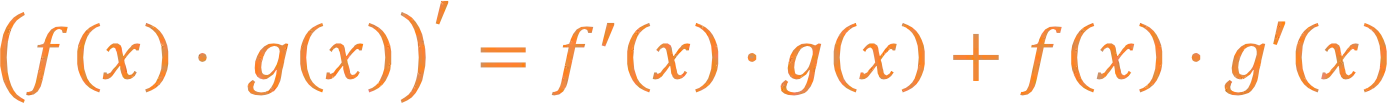
Regra do Produto
Regra do Produto

Ou seja, a regra do produto diz que a derivada do produto de duas funções é igual a multiplicação entre a primeira função e a derivada da segunda função mais a multiplicação da segunda função e a derivada da primeira função.

Parece um trava língua! Eu sei! 🤣 Mas calma, a gente vai fazer uns exemplos e tudo vai ficar mais claro!

📢 Clique para saber mais:

Como usar a Regra do Produto

Pra a gente aprender como usar a Regra do Produto, vamos fazer o exemplo que vimos lá em cima!

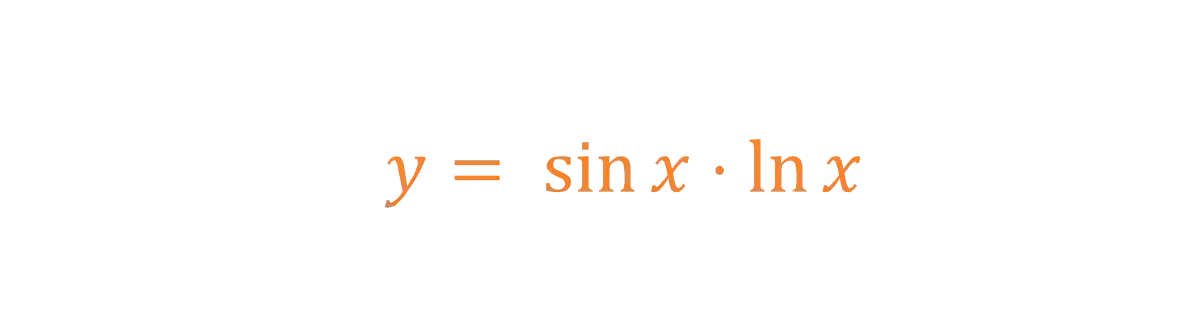
Produto de duas funções
Produto de duas funções

A resolução desse exemplo e muito mais, você pode conferir nesse vídeo que o Responde Aí preparou com todo o carinho pra você! 🧡 👇

Regra do Quociente

A Regra do Quociente é tão importante quanto a Regra do Produto! Aqui, como o próprio nome sugere, a gente vai derivar uma função que é igual a divisão de duas outras funções, como por exemplo:

A fórmula da regra do quociente é:

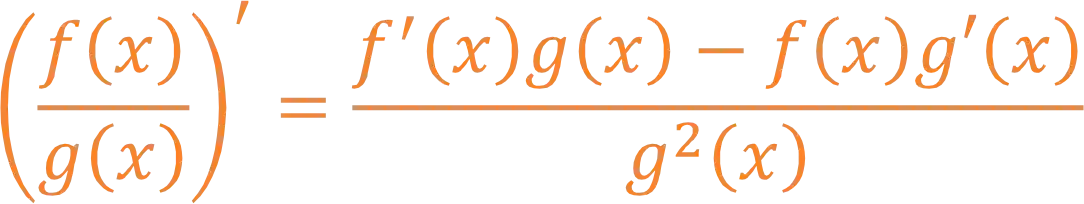
Regra do quociente
Regra do quociente

Como usar a Regra do Quociente?

Bora resolver nosso exemplo pra aprender como usar a regra do quociente!

Substituindo na regra do quociente:

Resolvendo, temos:

Ficou com alguma dúvida?! Se liga nesse resumo em vídeo da Regra do Quociente 👇

Agora vamos praticar com exercícios?

Regra do Quociente

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Encontre a derivada da função:

y = s e n ( x ) cos ⁡ x

Passo 1

Lembrando da regra do produto

f g ' = f ' g + f g '

Obtemos:

y ' = s e n ( x ) ' cos ⁡ x + s e n x   cos ⁡ x '

Passo 2

Substituindo as derivadas:

y ' = cos ⁡ x cos ⁡ x + s e n ( x ) - s e n ( x )

y ' = cos 2 ⁡ ( x ) - sen 2 ⁡ ( x )

Resposta

y ' = cos 2 ⁡ ( x ) - sen 2 ⁡ ( x )

Exercício Resolvido #2

George B. Thomas Jr., Cálculo volume I, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp.220-24

No exercício, determine a derivada de y em relação a x , conforme o caso:

y = x 3 3 ln ⁡ x - x 3 9

Passo 1

Temos que derivar esse cara aplicando a Regra do Produto no primeiro termo e derivando direto no segundo. Da Regra do Produto, temos:

f g ' = f ' g + f g '

A derivada de y , pelas propriedades de derivação, será:

y ' = x 3 3 ln ⁡ x ' - x 3 9 '

Passo 2

Então, a primeira derivada fica:

x 3 3 ln ⁡ x ' = x 3 3 ' ln ⁡ x + x 3 3 ln ⁡ x '

= 3 x 2 3 ln ⁡ x + x 3 3 1 x

= x 2 ln ⁡ x + x 2 3

Passo 3

Para a segunda derivada, fazemos pela derivada do polinômio direto:

x 3 9 ' = 3 x 2 9

= x 2 3

Logo,

y ' = x 3 3 ln ⁡ x ' - x 3 9 '

= x 2 ln ⁡ x + x 2 3 - x 2 3

= x 2 ln ⁡ x

Resposta

y ' = x 2 ln ⁡ x

Exercício Resolvido #3

UNICAMP - Cálculo 1 - P1 2013.1 - 4 b

Calcule f ' ( x ) onde:

f x = ( cos ⁡ x ) ( 12 x + 3 x )

Passo 1

Para derivar isso aí basta a gente usar a Regra do Produto:

h g ' = h ' g + h g '

Escrevi com h e não f a fórmula da Regra do Produto para não confundir com o f da questão.

f ' x = cos ⁡ x ' 12 x + 3 x + cos ⁡ x 12 x + 3 x '

Passo 2

Vamos fazer os dois termos derivados e adicionar lá. Primeiro derivada do cosseno:

cos ⁡ x ' = - sen ⁡ x

Agora para derivar o outro termo temos um polinômio e uma exponencial. Pela definição, derivamos assim:

12 x + 3 x ' = ln ⁡ ( 12 ) 12 x + 3

Passo 3

Junta tudo agora:

f ' x = cos ⁡ x ' 12 x + 3 x + cos ⁡ x 12 x + 3 x '

- sen ⁡ x 12 x + 3 x + cos ⁡ x ln ⁡ 12 12 x + 3

Resposta

f ' x = - sen ⁡ x 12 x + 3 x + cos ⁡ x ln ⁡ 12 12 x + 3

Exercício Resolvido #4

Elaboração Própria

Calcule a derivada da função abaixo:

y = x 2 x + 2 ( x 3 + 1 )

Passo 1

Como se trata de um produto de 3 funções, vamos utilizar a regra do produto para 3 termos:

y ' = f   x g x h x '

y ' = f ' x ∙ g x ∙ h x + f x ∙ g ' x ∙ h x + f x ∙ g x ∙ h ' x

Vamos agora derivar cada uma das três.

f x = x 2

g x = x + 2

h x = x 3 + 1

Passo 2

Derivando f x , g x e h x :

f ' x = x 2 ' = 2 x

g ' x = x + 2 ' = 1 2 x 1 2 - 1 + 0 = 1 2 x

h ' x = x 3 + 1 ' = 1 3 x - 2 3 + 0 = 1 3 x - 2 3 = 1 3 x 2 3

Passo 3

Aplicando isso na fórmula do Passo 1 teremos:

y ' = f ' x ∙ g x ∙ h x + f x ∙ g ' x ∙ h x + f x ∙ g x ∙ h ' x

Então, cada um desses três termos vai ficar:

f ' x ∙ g x ∙ h x = 2 x x + 2 ( x 3 + 1 )

f x ∙ g ' x ∙ h x = x 2 1 2 x ( x 3 + 1 )

f x ∙ g x ∙ h ' x = x 2 x + 2 1 3 x 2 3

Como y ' é a soma desses três pedacinhos:

y ' = 2 x x + 2 x 3 + 1 + x 2 1 2 x x 3 + 1 + x 2 x + 2 1 3 x 2 3

Resposta

y ' = 2 x x + 2 x 3 + 1 + x 2 1 2 x x 3 + 1 + x 2 x + 2 1 3 x 2 3

Exercício Resolvido #5

UNICAMP - Cálculo 1 - Exame 2012 Noturno - 1 b

Calcule:

g ' x ,     s e   g x = 1 - e x 1 + e x

Passo 1

Derivamos esse cara pela Regra do Quociente:

g ' x = 1 - e x ' 1 + e x - 1 - e x 1 + e x ' 1 + e x 2

Passo 2

Como a derivada de e x é o próprio e x , teremos:

1 - e x ' = - e x         ;         1 + e x ' = e x

Passo 3

Substituindo

= - e x 1 + e x - 1 - e x e x 1 + e x 2

= - e x - e 2 x - e x + e 2 x 1 + e x 2

= - 2 e x 1 + e x 2

É isso!

Resposta

g ' x = - 2 e x 1 + e x 2

Exercício Resolvido #6

Elaboração Própria

Calcule a derivada da seguinte função:

y = ln ⁡ x - x x + x 2

Passo 1

Assim como derivada da soma é a soma das derivadas, a derivada da subtração é a subtração das derivadas:

y ' = ln ⁡ x ' - x x + x 2 '

Agora, nós podemos resolver as duas derivadas separadamente.

Passo 2

A derivada do logaritmo nós conhecemos:

ln ⁡ x ' = 1 x

Passo 3

De resto temos que usar a regra do quociente:

f g ' = f ' g - f g ' g 2

x x + x 2 ' = x ' x + x 2 - x x + x 2 ' x + x 2 2

Agora vamos calcular as derivadas:

x x + x 2 ' = x + x 2 - x 1 2 x - 1 2 + 2 x x + x 2 2

Pronto! Mas ainda podemos melhorar a cara dessa derivada, aplicando a distributiva em x 1 2 x - 1 2 + 2 x e depois fazendo a subtração:

x x + x 2 ' = x + x 2 - x 2 + 2 x 2 x + x 2 2 = x 2 - x 2 x + x 2 2

Passo 4

Agora que calculamos as derivadas em separado, vamos subtrair tudo:

y ' = ln ⁡ x ' - x x + x 2 '

= 1 x - x 2 - x 2 x + x 2 2

Resposta

y ' = 1 x - x 2 - x 2 x + x 2 2

Exercício Resolvido #7

Elaboração Própria

Calcule a derivada da função definida abaixo:

y = x s e n ( x ) + x 2

Passo 1

Aplicando a regra do quociente:

f g ' = f ' g - f g ' g 2

Nós chegamos a:

y ' = x ' s e n ( x ) + x 2 - x s e n ( x ) + x 2 ' s e n ( x ) + x 2 2

Passo 2

Calculando as derivadas:

x ' = 1 2 x 1 2   - 1 = 1 2 x - 1 2

Temos também:

s e n ( x ) + x 2 ' = cos ⁡ x + 2 x

Passo 3

Finalmente, substituindo:

y ' = 1 2 x - 1 2 s e n ( x ) + x 2 - x cos ⁡ x + 2 x s e n ( x ) + x 2 2

Colocando 1 2 em evidência:

y ' = 1 2 x - 1 2 sen ⁡ x + x 2 - 2 x cos ⁡ x + 2 x sen ⁡ x + x 2 2

Resposta

y ' = x - 1 2 sen ⁡ ( x ) + x 2 - 2 x cos ⁡ x + 2 x 2 sen ⁡ ( x ) + x 2 2

Exercício Resolvido #8

UNICAMP - Cálculo 1 - P1 2013.1 - 4 a

Calcule f ' ( x ) onde:

a   f x = x + sen ⁡ x 4 x + x

Passo 1

Temos um quociente, adivinha que regra começamos usando? Duuh, a do Quociente.

f ' x = x + sen ⁡ x ' 4 x + x - x + sen ⁡ x 4 x + x ' 4 x + x 2

Passo 2

Agora calculamos as duas derivadas que ficaram sobrando do outro termo. Uma de cada vez:

x + sen ⁡ x ' = x 1 2 ' + sen ⁡ x ' = 1 2 x - 1 2 + cos ⁡ x

4 x + x ' = ln ⁡ ( 4 ) 4 x + 1

Passo 3

Vamos aglomerar tudo na fórmula original:

f ' x = x + sen ⁡ x ' 4 x + x - x + sen ⁡ x 4 x + x ' 4 x + x 2

= 1 2 x - 1 2 + cos ⁡ x 4 x + x - x + sen ⁡ x ln ⁡ 4 4 x + 1 4 x + x 2

Resposta

f ' x = 1 2 x - 1 2 + cos ⁡ x 4 x + x - x + sen ⁡ x ln ⁡ 4 4 x + 1 4 x + x 2

Exercícios de Livros Relacionados

Se h 2 = 4 e h ' 2 = - 3 , encontre d d x h x x | x = 2
Se f x = e x g x , onde g 0 = 2 e g ' 0 = 5 , encontre f ' 0 .
Se g for uma função derivável, encontre uma expressão para derivada de cada uma das seguintes funções. y = x g ( x ) y = x g x y = g x x
62. a) Se F x = f x g x , onde f e g tên derivadas de todas as ordens, mostre que F ' ' = f ' ' g + 2 f ' g ' + f g ' ' . b) Encontre fórmulas análogas para F ' ' ' e F 4 .c) Conjecture uma fórmula pa
Derive a função: R t = ( t + e t ) ( 3 - t )