Campos e Operadores Vetoriais
Teoria
Campos Vetoriais
Hoje será um dia que vai marcar sua vida! Eu tenho que te contar um segredo: tudo que você estudou até hoje estava relacionado a funções escalares. Oi? Função escalar é tipo , para cada valor de , temos uma resposta em número, tipo, sei lá,
Hoje, nós vamos dar um valor e recuperar um vetor! UAU!
Confuso? Sei que é meio abstrato, então vamos ver uns exemplos aqui!
Exemplos de campos vetoriais
1- Vamos começar com um bem simples:
Vamos conferir alguns valores, por exemplo:
E por aí vai. Cada ponto terá um vetor correspondente. Se fizermos uma quantidade boa de pontos, vamos ter algo assim:
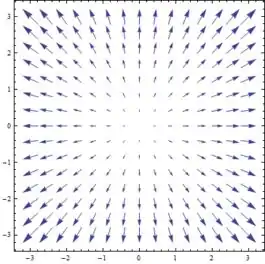
2- Agora um pouquinho mais complicado:
Vamos ver um ponto específico de novo
De novo, substituindo vários pontos vamos ter o gráfico abaixo:
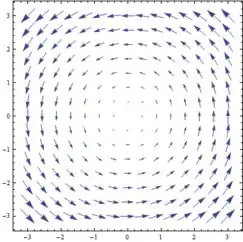
Bem diferente do primeiro campo lá em cima.
Mas não para por aí! Podemos criar qualquer tipo de campo. Nos exemplos acima a gente vê uma estrutura que se repete: todo campo é da forma
com e funções escalares de e , ou até mesmo constantes. Podemos ter:
Todos campos vetoriais diferentes.
Introdução aos Operadores
Agora que nós temos uma ideia do que são campos vetoriais, precisamos introduzir outros conceitos pra que possamos entender algumas de suas propriedades.
Na verdade, nesse tópico, só precisamos de um operador para obtermos tudo que queremos do campo. Ele é representado pela letra grega , o nome do símbolo é nabla, mas o operador se chama “del”.
Operador del
Então gente está na hora de conhecermos esse tal de del
Ele parece um vetor, mas não é não. Na verdade, ele é um operador, isso quer dizer que ele realiza alguma tarefa, mas não tem um significado propriamente dito.
Rotacional e Divergente
Então como eu falei lá em cima, o del só realiza tarefas. A primeira tarefa que a gente já viu ele fazendo é nos dar o vetor gradiente. Para isso, bastava aplica-lo numa função escalar
Recentemente, aprendemos o que é um campo vetorial. Agora é hora de ver as tarefas que o del pode fazer nesses campos. Para ilustrar vamos considerar o seguinte campos
A primeira tarefa que podemos fazer é um produto escalar, dessa forma aqui
Esse cara, é denominado divergente do campo , nós o representamos por .
Se fizemos um produto escalar, agora é normal pensar em fazer o produto vetorial. Vamos lá
Esse carinha, , é denominado rotacional do campo e nós o representamos por
Fica bem esperto com a diferença entre eles. O divergente é sempre um número, porque foi obtido de um produto escalar. Já o rotacional, que foi obtido de um produto vetorial, é sempre um vetor.
Então para ficar bem claro para você, se
- Divergente:
- Rotacional:
Agora vou te dar uma definição. Se o campo tiver rotacional nulo, ou seja, então ele é dito irrotacional. Se, por outro lado, o divergente for nulo, ou seja, , então ele é dito solenoidal.
Como eu sou teu amigo, vou te contar um segredo: e se o campo não tiver 3 componentes, ou seja, e se ? Então a gente simplifica bastante as coisas e usa o seguinte
Destrói os exercícios!
Introdução aos Operadores
Operador del
Rotacional e Divergente
Exercícios Resolvidos
Exercício Resolvido #1
George B. Thomas, Cálculo – volume 2, 11ª edição, São Paulo: Pearson Education do Brasil ltda., 2009, pp. 474-32.
Desenhe o campo radial
Juntamente com suas componentes verticais e horizontais em um conjunto representativo de pontos da circunferência
Passo 1
Então, pessoal, aqui para podermos desenhar o campo radial, vamos antes ter que entender como é o conjunto e definir alguns pontos para representar. Ele também forneceu as componentes horizontais e verticais, e a partir delas conseguimos traçar a resultante e desenhar o campo radial.
Como o exercício pede um conjunto representativo na cicunferência , podemos representar os pontos em que a circunferência corta os eixos e . Esses pontos seriam:
Mas também precisamos entender como é esse campo, quando não estamos em cima do eixo. Neste caso, podemos escolher os pontos “médios”, onde e são iguais em módulo:
Então a figura do conjunto representativo com os pontos selecionados ficou assim:
É valido ressaltar aqui, que poderiaos escolher outros pontos para desenhar, mas eles teriam que estar sobre a linha pontilhada azul da circunferência.
Passo 2
O enunciado forneceu esse campo radial:
Ou seja, as componentes horizontais são dadas por , e verticais, dadas por . Nesse caso temos e .
Então para cada um dos pontos vamos ter:
Então vamos desenhar cada uma das componentes:
Passo 3
O nosso objetivo aqui é desenhar o campo radial, então vamos achar a resultante dessas componentes. Ficará assim:
Finalmente, vamos ter os vetores definitivos, em vermelho; e as componentes, em amarelo.
Pronto, tudo feito!
Resposta
Exercício Resolvido #2
George B. Thomas, Cálculo – volume 2, 11ª edição, São Paulo: Pearson Education do Brasil ltda., 2009, pp. 474-32.
Desenhe o campo radial
Juntamente com suas componentes verticais e horizontais em um conjunto representativo de pontos da circunferência
Passo 1
O exercício pede um conjunto representativo na cicunferência , então acho que podemos escolher os pontos sobre o eixo:
E os pontos “médios”, onde e são iguais em módulo:
Por enquanto, vamos ter:
Passo 2
Agora, em cada um desses pontos, vamos traçar as componentes horizontais, dadas por , e verticais, dadas por .
Nesse caso temos
Que parece meio complicado, mas não é tanto, já que na circunferência , então basicamente temos e , o que nos dá:
Então vamos desenhar cada uma das componentes:
Agora é só somar as componentes e traçar o vetor final!
Passo 3
Finalmente, vamos ter os vetores definitivos, em vermelho; e as componentes, em amarelo:
Pronto, tudo feito!
Resposta
Exercício Resolvido #3
Hamilton Luiz Guidorizzi, Um Curso de Cálculo – volume 3, 5ª edição, Rio de Janeiro: LTC, 2001, pp. 20-1d,e.
Calcule o rotacional:
Passo 1
a)
Na teoria, a gente viu que o rotacional é cálculado a partir de:
Ou seja, o produto vetorial do operador com o campo vetorial. Onde, pra quem não lembra:
Então, vamos ter algo assim:
Trabalho braçal, galera! Vamos as contas!
Passo 2
b)
De novo, a mesma fórmula do item a):
E calculamos o produto vetorial:
Passo 3
c)
E mais uma vez, fazemos:
Sem mistério, né? Mas ainda faltam duas, não vamos perder o ânimo não!
Passo 4
d)
O campo aqui é bidimensional, então vou usar aquele segredo que te contei na teoria
Não esquece que o rotacional é um vetor, então tem que colocar aquele para não tomar errado na questão.
Passo 5
e)
Por último, finalmente, temos mais um campo bidimensional:
Ufa, quanta conta! Mas nada que não deu pra fazer, né?
Resposta
Exercício Resolvido #4
Hamilton Luiz Guidorizzi, Um Curso de Cálculo – volume 3, 5ª edição, Rio de Janeiro: LTC, 2001, pp. 30-1.
Calcule o divergente do campo vetorial dado.
Passo 1
a)
A gente viu na teoria que o divergente é, simplesmente:
Ou seja, o produto escalar do operador com o campo vetorial. Onde, pra quem não lembra:
Como nosso campo aqui é bidimensional, vamos usar só as duas primerias componentes e calcular as derivadas:
Passo 2
b)
Vamos repetir a fórmula do item a):
Mas agora temos um capo vetorial tridimensional, então vamos usar o operador completo:
Algumas derivadas mais
Passo 3
c)
Parece que a questão complicou um pouco agora, mas a fórmula é sempre a mesma, não esqueça:
Algumas derivadas não tão triviais quanto as anteriores, mas nada que você não saiba calcular, né?
Passo 4
d)
Pra terminar, temos um campo meio estranho, com uma componente em só. Mas nada impede de aplicarmos a fórmula:
Eita, agora sim uma derivada chata, mas vamos pela regra do produto e da cadeia:
Ficou feio, mas as vezes é assim mesmo, fazer o que...
Resposta
Exercício Resolvido #5
Hamilton Luiz Guidorizzi, Um Curso de Cálculo – volume 3, 5ª edição, Rio de Janeiro: LTC, 2001, pp. 203-6.
Seja
Determine para que seja solenoidal. Desenhe o campo para o determinado.
Passo 1
Como vimos na teoria, um campo vetorial é chamada de solenoidal se seu divergente vale .
Ou seja:
Então, é só calcular o produto escalar e resolver a equação para encontrarmos .
Então vamos lá!
Passo 2
Precisamos calcular as derivadas parciais:
Que parecem bem bizarras, mas saem pela regra do quociente, certo?
Um algebrismo meio chato, mas por sorte, podemos repetí-lo para , é só substituir o que é por e vice-versa. Aí temos:
Passo 3
Agora é somar e ver no que dá:
Tudo isso pra dar no final, que raiva, né? haha