Campos e Operadores Vetoriais
Produzido por Arthur Melo de AlmeidaTeoria
Campos Vetoriais
Hoje será um dia que vai marcar sua vida! Eu tenho que te contar um segredo: tudo que você estudou até hoje estava relacionado a funções escalares. Oi? Função escalar é tipo , para cada valor de , temos uma resposta em número, tipo, sei lá,
Hoje, nós vamos dar um valor e recuperar um vetor! UAU!
Confuso? Sei que é meio abstrato, então vamos ver uns exemplos aqui!
Exemplos de campos vetoriais
1- Vamos começar com um bem simples:
Vamos conferir alguns valores, por exemplo:
E por aí vai. Cada ponto terá um vetor correspondente. Se fizermos uma quantidade boa de pontos, vamos ter algo assim:
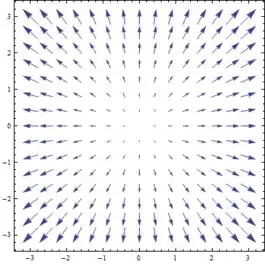
2- Agora um pouquinho mais complicado:
Vamos ver um ponto específico de novo
De novo, substituindo vários pontos vamos ter o gráfico abaixo:
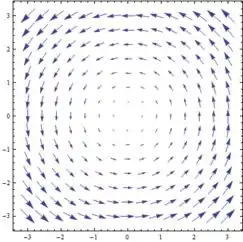
Bem diferente do primeiro campo lá em cima.
Mas não para por aí! Podemos criar qualquer tipo de campo. Nos exemplos acima a gente vê uma estrutura que se repete: todo campo é da forma
com e funções escalares de e , ou até mesmo constantes. Podemos ter:
Todos campos vetoriais diferentes.
Introdução aos Operadores
Agora que nós temos uma ideia do que são campos vetoriais, precisamos introduzir outros conceitos pra que possamos entender algumas de suas propriedades.
Na verdade, nesse tópico, só precisamos de um operador para obtermos tudo que queremos do campo. Ele é representado pela letra grega , o nome do símbolo é nabla, mas o operador se chama “del”.
Operador del
Então gente está na hora de conhecermos esse tal de del
Ele parece um vetor, mas não é não. Na verdade, ele é um operador, isso quer dizer que ele realiza alguma tarefa, mas não tem um significado propriamente dito.
Rotacional e Divergente
Então como eu falei lá em cima, o del só realiza tarefas. A primeira tarefa que a gente já viu ele fazendo é nos dar o vetor gradiente. Para isso, bastava aplica-lo numa função escalar
Recentemente, aprendemos o que é um campo vetorial. Agora é hora de ver as tarefas que o del pode fazer nesses campos. Para ilustrar vamos considerar o seguinte campos
A primeira tarefa que podemos fazer é um produto escalar, dessa forma aqui
Esse cara, é denominado divergente do campo , nós o representamos por .
Se fizemos um produto escalar, agora é normal pensar em fazer o produto vetorial. Vamos lá
Esse carinha, , é denominado rotacional do campo e nós o representamos por
Fica bem esperto com a diferença entre eles. O divergente é sempre um número, porque foi obtido de um produto escalar. Já o rotacional, que foi obtido de um produto vetorial, é sempre um vetor.
Então para ficar bem claro para você, se
- Divergente:
- Rotacional:
Agora vou te dar uma definição. Se o campo tiver rotacional nulo, ou seja, então ele é dito irrotacional. Se, por outro lado, o divergente for nulo, ou seja, , então ele é dito solenoidal.
Como eu sou teu amigo, vou te contar um segredo: e se o campo não tiver 3 componentes, ou seja, e se ? Então a gente simplifica bastante as coisas e usa o seguinte
Destrói os exercícios!