14.18. Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa para traçar gráficos tridimensionais no computador, utilize-o com a janela de inspeção e o ponto de vista que mostre os aspectos importantes da função.

Vamos começar determinando nossas derivadas:

Vamos derivar primeiro em relação à , vamos usar a regra do produto para derivar. A regra do produto é a seguinte:

Mas antes de tudo, repare que é uma constante, então podemos fazer o seguinte

Agora podemos fazer a regra do produto.

Vamos fazer

Então

E

Então

Agora a gente pode fazer a derivada:

Simplificando:

Agora a gente faz a derivada em relação a , e vamos usar a mesma estratégia, regra do produto:

Agora é constante, então:

Vamos fazer:

Então:

E

Então:

Agora a gente pode fazer a derivada:

Simplificando:

Beleza, agora a gente já tem nossas derivadas, os pontos interessantes vão acontecer quando elas forem iguais à 0. Então

Vamos lá, nas duas equações, veja que se

não importa o valor de , o resultado é , então pontos do tipo

são pontos críticos.

Para além disso, se

Então

logo,

vamos substitui isso em , veja que como está elevado ao quadrado, não importa se seu valor é positivo ou negativo

Isso só é se

Então

então temos outros quatro pontos críticos

Ou

Já temos nossos pontos de interesse, mas falta dizer se são máximos, mínimos ou pontos de sela, para isso a gente precisa da segunda derivada, vamos usar

Podem ocorrer três casos:

1. então é um mínimo local.
2. então é um máximo local.
3. então não é nem mínimo e nem máximo local.

Vamos calcular as segundas derivadas então

Agora derivamos isso em relação a

A outra derivada que precisamos é

Derivando em relação a

E a última derivada que precisamos é

ou

Vamos derivar isso em relação a

Então

Essa equação ficou grandinha né?

Vamos testar para o ponto

Já vou colocar as respostas direto para a gente não ficar fazendo aquelas equações gigantes.

Então temos que analisar :

Então é um ponto de mínimo.

Pelas configurações de , todo está elevado à um número par, então vai dar a mesma coisa para o ponto e coincidentemente vai dar o mesmo resultado para o ponto .

A gente cortou um caminho, mas ainda faltam infinitos pontos para a gente analisar, literalmente, os pontos do tipo , mas vamos tentar não fazer tantas contas.

Nossa função é

Se

então

exceto se

nesse caso

então vemos que quando

e

temos um valor menor para essa função do que qualquer outro ponto onde e , então para são todos pontos de mínimo.

Agora vamos pensar para

Então

de novo, exceto se

nesse caso

então vemos que quando

e

temos um valor maior para essa função do que qualquer outro ponto onde

e ,

então para são todos pontos de máximo.

Dadas essas condições, o ponto tem que ser necessariamente um ponto de sela.

Agora só falta fazer o gráfico.

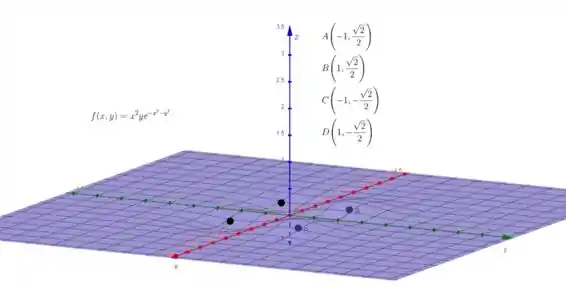
A gente gerou o grafico com o geogebra, para melhor visualização.