Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.1 - Ex. 8
15.8. A figura mostra curvas de nível da função f no quadrado . Use-as para estimar com precisão nas unidades.
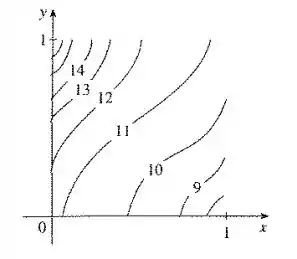
Passo 1
Para estimar essa integral dupla precisamos usar o teorema do ponto médio.
A gente tem que repartir a figura em subretângulos. Para começar vamos fazer para um único subretângulo. Esse Subretângulo, teria área igual a 1.
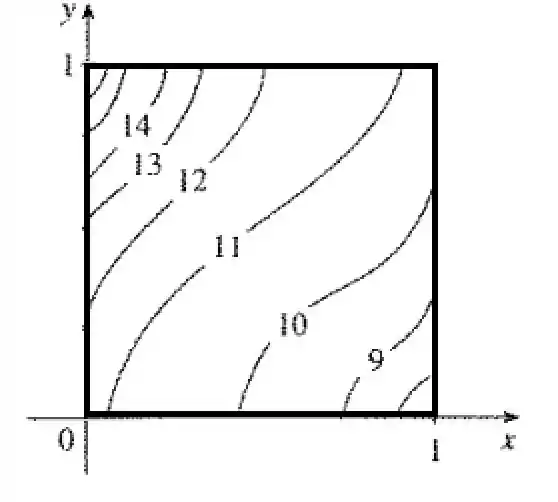
E o único ponto médio é . A linha do 11 passa mais ou menos ali no meio.
Os limites são, 1 retângulo para e 1 para .
Então nossa aproximação fica
Passo 2
Mas precisamos dar uma precisão maior para o nosso problema, então vamos separar em mais subretângulos, 4 dessa vez
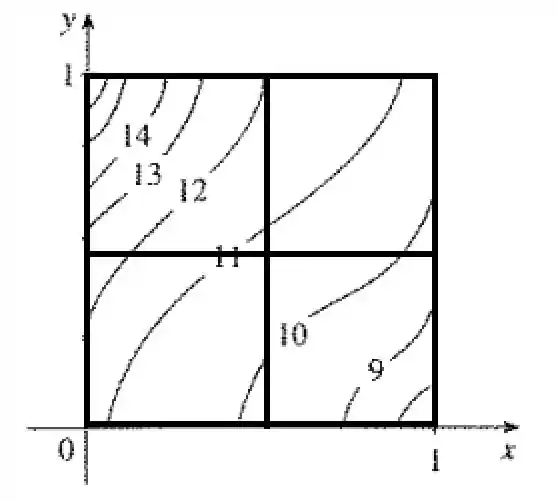
Agora a área dos retângulos é
Os limites são, 2 retângulos para e 2 para .
E temos
O resultado na verdade seria mas isso é aproximadamente .
Passo 3
Vamos aumentar mais ainda nossa precisão, separando agora em 16 subretângulos.
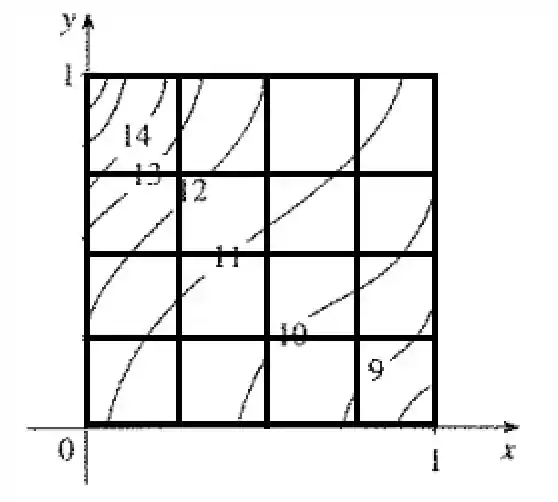
Agora a área dos retângulos é
Os limites são, 4 retângulos para e 4 para .
E temos