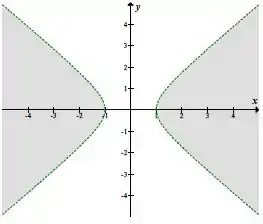
25. Esboçar a região de continuidade das seguintes funções:
a)
Passo 1
Ao analisar a função dada, temos que procurar em quais pontos ela não é continua, ou seja, procure as partes onde eu o domínio não existe para te ajudar na hora de montar o gráfico.
Sabemos que não pode haver raiz de números negativos, portanto meu denominador tem que ser positivo:
Isso ocorre, sempre que:
Interpretando graficamente em questão de domínio, temos uma parábola deitada, cortando o eixo no . Como estamos mexendo com função de segundo grau, temos essa interpretação para ambos os lados do eixo.
Como meu numerador é sempre uma função polinomial, ela está contida em todo o domínio dos reais, não interferindo no nosso gráfico de continuidade.
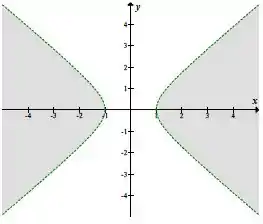
Resposta