Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 3.3 - Ex. 51

A figura mostra um arco de círculo com comprimento s e uma corda com comprimento d , ambos subentendidos por um ângulo central θ . Encontre

lim θ → 0 + ⁡ s d

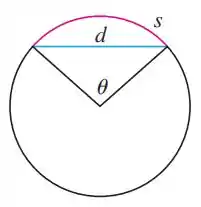
Passo 1

Eaee, belezinha?? Bom... queremos encontrar o seguinte limite:

lim θ → 0 + ⁡ s d

Sabendo que s , d e θ são mostrados na figura abaixo:

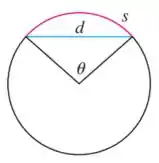
Para resolver esse limite, devemos relacionar s e d com θ .

Seja r o raio da circunferência:

s = r θ

E como a bissetriz do ângulo forma um triângulo retângulo, vale a relação trigonométrica:

sen ⁡ θ 2 = d 2 r ∴

d = 2 r sen ⁡ θ 2

Agora sim!! Bora atrás de aplicar no limite!! 😉

Passo 2

Então, a razão é dada por:

s d = r θ 2 r sen ⁡ θ 2 ∴

s d = θ 2 sen ⁡ θ 2 ∴

s d = θ 2 sen ⁡ θ 2

Passo 3

Logo, aplicando no limite, temos:

lim θ → 0 + ⁡ s d = lim θ → 0 + ⁡ θ 2 sen ⁡ θ 2 ∴

lim θ → 0 + ⁡ s d = lim θ → 0 + ⁡ 1 sen ⁡ θ 2 θ 2  

Passo 4

Para lim θ → 0 + ⁡ sen ⁡ θ 2 θ 2 , aplicando a mudança de variáveis w = θ 2 de modo que quando θ → 0 + então w → 0 e θ ≠ 0 implica em w ≠ 0 , logo:

lim θ → 0 + ⁡ sen ⁡ θ 2 θ 2 = lim w → 0 ⁡ sen ⁡ w w

Com base no limite fundamental lim w → 0 ⁡ sen ⁡ w w = 1 temos então:

lim θ → 0 + ⁡ sen ⁡ θ 2 θ 2 = 1

Logo:

lim θ → 0 + ⁡ s d = lim θ → 0 + ⁡ 1 sen ⁡ θ 2 θ 2 ∴

lim θ → 0 + ⁡ s d = 1 1 ∴

lim θ → 0 + ⁡ s d = 1

Resposta

lim θ → 0 + ⁡ s d = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o limite a seguir lim x → 0 ⁡ xc o s s e c2 xcos ⁡ 5 x
Determine o limite a seguir lim x → 0 ⁡ t g2 x x
Determine o limite a seguir lim t → 0 ⁡ 2 t t gt
Determine o limite a seguir lim t → 0 ⁡ s e nk t t( kc o n s t a n t e )
Determine o limite a seguir lim h → 0 - ⁡ h s e n3 h