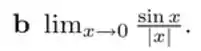Exercícios de Limite Fundamental Trigonométrico - Lista de Exercícios Resolvida
Questão 5
Calcule o limite, se possível. Caso conclua que o limite não existe, justifique.
Ver solução completaQuestão 7
Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.
Ver solução completaQuestão 8
Calcule o limite, se possível. Caso conclua que o limite não existe, justifique.
Ver solução completaQuestão 10
Calcule o limite, se possível. Caso conclua que não existe, justifique.
Ver solução completaQuestão 19
Calcule ou mostre que não existe. (Não use qualquer artifício que envolva derivação).
Questão 20
Calcule ou mostre que não existe. (Não use qualquer artifício que envolva derivação).
Questão 26
Calcule, se existir, o valor dos seguintes limites. Caso não exista, justifique.
Ver solução completaQuestão 29
Calcule, sem usar regra de L’Hôspital, os limites abaixo ou prove que não existe. Justifique suas respostas:
- Seja uma função tal que para todo . Usando o teorema do confronto, calcule o limite (e justifique)
Questão 33
Questão 1. Avalie os limites abaixo e encontre o correspondente valor caso exista. justifique suas respostas.
b)
Ver solução completaQuestão 35
Calcule o limite, se possível. Caso conclua que não existe, justifique.
Ver solução completaQuestão 37
Calcule ou argumente que os valores não existem. Em todos os casos justifique seus cálculos e respostas.
Ver solução completaQuestão 41
1b) Determine se existem ou não os seguintes limites. Em caso afirmativo, calcule o seu valor. (Justifique!)(NÃO é permitido uso da regra de L’Hôspital)
Ver solução completaQuestão 48
Calcule o seguinte limite : (NÃO é permitido o uso da Regra de L’Hôpital)
Ver solução completaQuestão 56
Calcule o limite, se possível. Caso conclua que não existe, justifique.
Ver solução completaQuestão 71
Calcule ou mostre que não existe.
Restrição: o uso da Regra de L’Hôpital só poderá ser utilizado em apenas um dos itens.
Ver solução completaQuestão 74
Calcule o limite, se possível. Caso conclua que não existe, justifique.
Ver solução completaQuestão 83
11) Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.
Ver solução completaQuestão 84
12) Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.
Ver solução completaQuestão 85
13) Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.
Ver solução completaQuestão 86
14) Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.
Ver solução completaQuestão 90
Calcule ou mostre que não existe. (Não use qualquer artifício que envolva derivação).
Questão 91
Seja ; onde são números reais e é um inteiro positivo. Dado que para todo número real ; utilize limite e/ou derivada para provar que:
Ver solução completaQuestão 92
Calcule ou mostre que não existe. (Não use qualquer artifício que envolva derivação).
Questão 93
Calcule ou mostre que não existe (Não use qualquer artifício que envolva derivada).
Questão 98
O limite trigonométrico fundamental nos diz que . Use essa informação para calcular os limites abaixo.
(a)
Ver solução completaQuestão 104
Calcule os seguintes limites, caso existir, justificando também se não existir
Ver solução completaQuestão 115
O limite trigonométrico fundamental nos diz que . Use essa informação para calcular os limites abaixo.
(b)
Ver solução completaQuestão 116
Calcule o limite, se possível. Caso conclua que não existe, justifique.
Ver solução completaQuestão 118
Calcule, sem usar regra de L’Hôspital, os limites abaixo ou prove que não existe. Justifique suas respostas:
- Seja uma função tal que para todo . Usando o teorema do confronto, calcule o limite (e justifique)
Questão 120
O limite trigonométrico fundamental nos diz que . Use essa informação para calcular os limites abaixo.
(c)
Ver solução completaQuestão 130
Q01b) Avalie os limites abaixo e encontre o correspondente valor caso exista. Justifique suas respostas:
Ver solução completaQuestão 132
Determine se existem ou não os seguintes limites. Em caso afirmativo, calcule o seu valor. (Justifique)! (NÃO é permitido o uso da regra de L’Hospital).
Questão 133
Avalie os limites abaixo e encontre o correspondente valor caso exista. Justifique suas respostas.
Ver solução completaQuestão 135
Calcule ou mostre que não existe (Não use qualquer artifício que envolva derivada).