Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.8 - Ex. 54

53-56Use os resultados do Exercício 52.

54.

(a)Confirme gráfica e algebricamente que 1 2 x + 1 ≤ e x 2 x + 1 ( x ≥ 0 )

(b)Calcule a integral ∫ 0 + ∞ 1 2 x + 1 d x

(c)O que o resultado obtido em (b) diz sobre a integral ∫ 0 + ∞ 1 2 x + 1 d x ?

Passo 1

(a)Temos, respectivamente, os gráficos das funções:

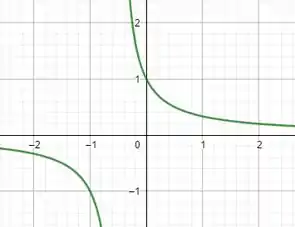
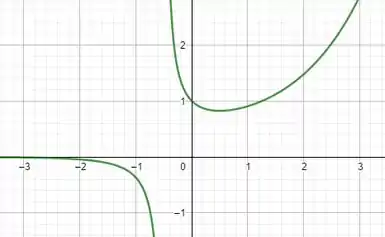
Confirmamos algebricamente que 1 2 x + 1 ≤ e x 2 x + 1 pra valores de x maiores ou iguais a zero quando comparamos 1 e e x .

Pra valores de x = 0 , e x = e 0 = 1 , que faz com que seja igual a 1 . A partir de x = 0 , e x só vai assumir valores maiores que 1 .

Passo 2

(b)Sendo o cálculo de uma integral imprópria, escrevemos ela na forma de limite, assim:

∫ 0 + ∞ 1 2 x + 1 d x = lim t → + ∞ ⁡ ∫ 0 t 1 2 x + 1 d x

Agora calculamos a integral normalmente. Temos:

∫ 0 t 1 2 x + 1 d x = 1 2 ∫ 0 t 2 2 x + 1 d x = 1 2 ∙ ln ⁡ ( 2 x + 1 ) 0 t

Aplicamos o TFC:

∫ 0 t 1 2 x + 1 d x = 1 2 ∙ ln ⁡ 2 t + 1 - ln ⁡ 2 ∙ 0 + 1 =

= 1 2 ∙ ln ⁡ 2 t + 1

Por fim, calculamos o limite:

∫ 0 + ∞ 1 2 x + 1 d x = lim t → + ∞ ⁡ ∫ 0 t 1 2 x + 1 d x = l i m t → + ∞ 1 2 ∙ ln ⁡ 2 t + 1 =

= 1 2 ∙ l i m t → + ∞ ln ⁡ 2 t + 1 = 1 2 ∙ ln ⁡ + ∞ =

= + ∞

A integral diverge, e não representa um valor numérico pra área.

Passo 3

(c)Como discutido no exercício 52, se a integral da função menor (no intervalo de integração observado) diverge, a integral da função maior, no mesmo intervalo deve também divergir.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da região que é delimitada pelo eixo x e a curva y = ln ⁡ x - 1 x 2 com x≥e .
Calcule a integral se for convergente. ∫ 0 1 1 2 x - 1 d x
Encontre o volume do sólido que é gerado quando a região entre a curva y = e - x com x ≥ 0 e o eixo x gira em torno do eixo y .
Com quais valores de integral ∫ 0 + ∞ e p x d x Converge?
Em cada item, tente calcular exatamente a integral com um CAS. Se sua resposta não for numericamente simples, então use o CAS para encontrar uma aproximação numérica da integral. ∫ 1 + ∞ s e nx x 2 d