Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.1 - Ex. 16
7-18 Esboce a região englobada pelas curvas e encontra a área
16.,
Passo 1
Vamos começar falando a fórmula que vamos usar nessa questão e lembrando que depois, teremos que fazer o esboço das curvas!
Essa fórmula é a 6.1.2 Fórmula para a área
Se e forem contínuas no intervalo e se em cada de , então a área da região limitada acima por , abaixo por , à esquerda pela reta e à direita pela reta é
Passo 2
Vamos começar desenhando nosso gráfico para assim vermos como a região é delimitada!
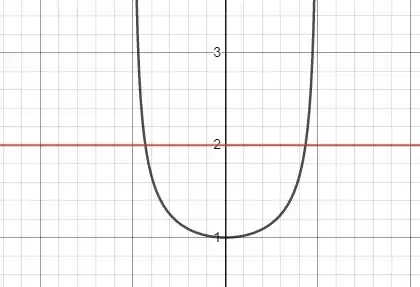
Em preto está a curva e em vermelho está a função .
Essa figura é simétrica em relação ao eixo , o que tem a direita é igual ao que tem à esquerda, então vamos fazer a integral pensando apenas na parte da direita e depois multiplicaremos por .
Quem delimita acima é a função e quem delimita à baixo é , então
Agora para descobrirmos quem delimita á direita, temos que igualar as duas funções, quem delimita à esquerda é . Vamos igualar:
Só que usaremos o , pois estamos no lado positivo de .
Portanto é delimitado à esquerda por e à direita por
Vamos montar a integral, lembrando que precisamos multiplicar por a expressão da área:
Passo 3
Paramos na expressão da integral, então voltaremos dela!
Vamos fazer primeiro a integral indefinda separadamente!
Então fazendo e , sabendo que
Voltando para a integral definida:
Então a área é: