Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.9 - Ex. 48

Ache a área da região acima da parábola x 2 = 4 p y e dentro do triângulo formado pelo eixo x e pelas retas y = x + 8 p e y = - x + 8 p .

Passo 1

Vamos olhar o gráfico das duas funções sobreposto um ao outro (sem perda de generalidade, para simplificar, vamos analisar o caso de p = 1 ):

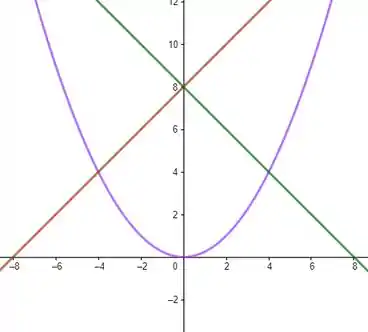
Passo 2

Seja A o ponto de interseção da reta y = x + 8 p com a parábola, e B o ponto de interseção y = - x + 8 p com a parábola

Vamos encontrar o ponto A :

y = x + 8 p x 2 = 4 p y

A = ( - 4 p , 4 p )

Vamos encontrar o ponto B:

y = - x + 8 p x 2 = 4 p y

B = ( 4 p , 4 p )

Passo 3

Para calcular a área S em questão, temos que resolver duas integrais, a primeira variando de A até a reta x = 0 , e a segunda variando da reta x = 0 até o ponto B.

S = ∫ - 4 p 0 x + 8 p - x 2 4 p d x + ∫ 0 4 p ( - x + 8 p - x 2 4 p ) d x

S = x 2 2 + 8 p x - x 3 12 p - 4 p 0 + - x 2 2 + 8 p x - x 3 12 p 0 4 p

S = 112 3 p 2

Resposta

A área S , em unidades de área do gráfico, é:

S = 112 3 p 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = e - x ,y = x + 1ex = - 1
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = sen ⁡ 2 x ,y = x + 2 ,x = 0ex = π / 2
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = 2 x , y = 2 - xey = 4
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = arcsen ⁡ x , y = π 2ex = 0
Calcular a área da região limitada pelas seguintes curvas, dadas na forma paramétrica. x = cos ⁡ t y = s e nt e x = cos ⁡ t y = 1 2 s e nt