Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 10

A base do sólido é a região encerrada por um círculo tendo um raio de r unidades, e toda a secção plana perpendicular a um diâmetro fixo da base é um quadrado cuja diagonal é uma corda do círculo. Ache o volume do sólido descrito.

Passo 1

Pessoal, para resolver essa questão nós vamos utilizar o método dos cortes e para utilizá-lo precisamos achar a fórmula da área de uma secção perpendicular genérica.

O problema disse que a base será a seguinte o círculo abaixo de raio r .

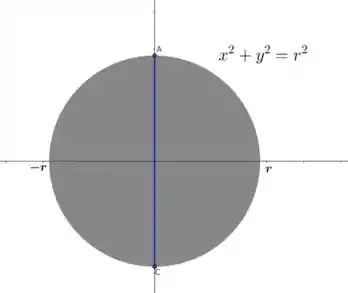
O problema também disse que a secção plana perpendicular ao eixo da base será um quadrado em que a diagonal será uma corda do círculo, ou seja, será a interseção da região com a secção plana. Sendo assim, na nossa representação acima, A C - seria a diagonal do quadrado que é a secção plana no x = 0 . Agora precisamos achar a fórmula da área de uma secção plana genérica.

Sendo a equação da circunferência x 2 + y 2 = r 2 , as equações das semi-circunferências serão:

y = r 2 - x 2             e           y = - r 2 - x 2

O comprimento do segmento A C - é justamente r 2 - x 2 - - r 2 - x 2 , considerando a abscissa genérica x . Então A C - = 2 r 2 - x 2 .

Perceba que A C - = 2 r 2 - x 2 é a diagonal de um quadrado genérico e lembrando que D i a g o n a l = 2 l , descobrimos que o lado do quadrado é:

l = A C - 2 = 2 2 r 2 - x 2 = 2 r 2 - x 2

l x = 2 r 2 - x 2

Logo, a área será:

A x = 2 ( r 2 - x 2 )

Passo 2

Agora, vamos lembrar a fórmula que calcula o volume. Seja S um sólido tal que S esteja entre planos perpendiculares ao eixo x em a e b . Se a medida da área da secção plana de S no plano perpendicular ao eixo x em x for dada por A ( x ) , onde A é contínua em [ a , b ] , então a medida do volume de S será dada por:

V = ∫ a b A ( x ) d x

Comparando com o nosso problema, o nosso sólido estará entre planos perpendiculares ao eixo x no intervalo [ - r , r ] , então esse será o nosso intervalo de integração. E também achamos a fórmula da área A x = 2 ( r 2 - x 2 ) das secções, logo, basta aplicar a fórmula.

V = ∫ - r r 2 ( r 2 - x 2 ) d x

Passo 3

Para calcular a integral, precisamos lembrar que ∫ x n d x = x n + 1 n + 1 + C       n ≠ - 1 .

Agora vamos resolver a definida utilizando a primitiva acima.

Sabemos da integral definida que:

∫ a b f x d x = F b - F a

Em que F é uma primitiva de f .

Dessa forma,

V = ∫ - r r 2 ( r 2 - x 2 ) d x = 2 r 2 x - x 3 3 - r r = 2 r 2 r - r 3 3 - 2 r 2 ( - r ) - ( - r ) 3 3

= 2 3 r 3 - r 3 3 - 2 - 3 r 3 + r 3 3 = 2 2 r 3 + 2 r 3 3 = 8 r 3 3

V = 8 r 3 3   u . v

O volume é 8 r 3 3 unidades de volume.

Resposta

V = 8 r 3 3   u . v

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . x + y = 4 , x = y 2 - 4 y + 4
Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . y = 4 - 2 x , y = 0 , x = 0 ; s o b r ex = - 1
Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . x = 2 y 2 , y ≥ 0 , x = 2 , s o b r ex = 2
Use o método de cascas cilíndricas para induzir o volume gerado girando a região delimitada pelas curvas dadas sobre o eixo especificado. y = x 3 , y = 8 , x = 0 ; s o b r ex = 3
Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . x = 2 y 2 , x = y 2 + 1 , s o b r ey = - 2