Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.4 - Ex. 13
Um besouro parte do centro de um relógio muito grande, ao meio-dia, e percorre o ponteiro dos minutos a uma velocidade de 1. Suponha que a origem das coordenadas está no centro do relógio. Dê as equações paramétricas para a posição do besouro em função do tempo. Esboce a curva descrita pelo besouro.
Passo 1
Beleza, saca só. Tem dois movimentos que temos que considerar:
- O movimento do besouro pelo ponteiro
- O movimento circular do ponteiro
Agora olha isso: uma circunferência pode ser parametrizada em relação ao parâmetro da seguinte forma, sendo seu raio:
Como nesse caso tanto o ângulo varia com o tempo (movimento do ponteiro) quanto a distância até a origem varia com o tempo (movimento do besouro). Vamos ter:
Partiu achar essas expressões então
Passo 2
Pra começar, o ponteiro dos minutos demora pra dar uma volta completa. Sendo assim:
Onde o sinal de serve pra indicar que varia no sentido horário. Daí, tiramos:
Como no instante inicial é meio dia, temos:
Agora, veja bem, o besouro se afasta do centro a uma velocidade de . Podemos ajustar essa velocidade para ficar com a mesma unidade de medida de tempo da velocidade angular e teremos:
Galera, essa velocidade nada mais é do que:
Como o besouro ta no centro no instante inicial, temos:
E pra fechar com chave de ouro, temos a parametrização final:
Só um detalhe importante. O ponteiro dos minutos tem um tamanho fixo . Portanto, o parâmetro não pode variar infinitamente se não o besouro sai do relógio! Sendo assim, temos um valor , dado por:
Sendo assim:
Passo 3
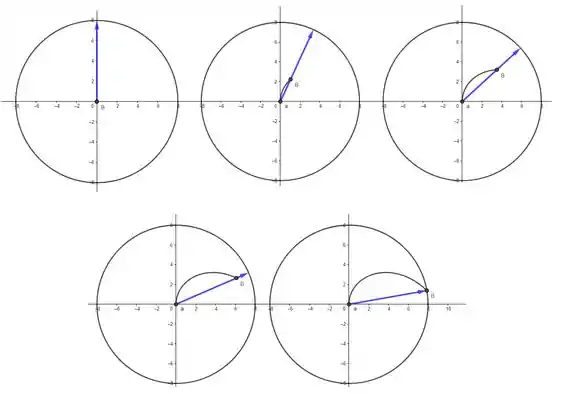
Um bom esboço pra trajetória seria:
Resposta
