Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.11 - Ex. 63a

Calcular a área entre as curvas:

  1. 2 r = 3 e r = 3 s e n theta

Passo 1

A área pedida está na figura:

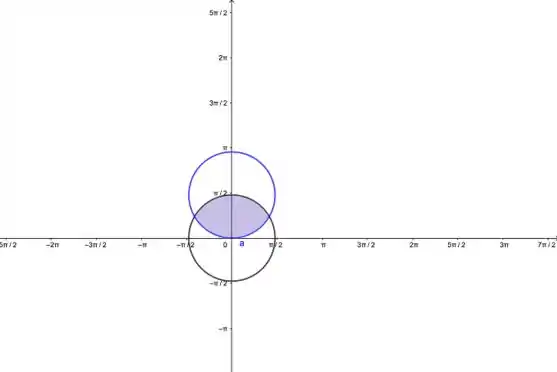
Vamos ver onde ocorre a interseções das funções:

(3)/(2) = 3 s e n theta

s e n theta = (1)/(2)

theta = (pi)/(6)

Porém, veja que até (pi)/(6) temos uma função (a de azul) que é r = 3 s e n theta e depois de (pi)/(6) até (pi)/(2) temos a outra função. E esse trecho é simétrico ao eixo y , então podemos fazer a área desses dois, somar e multiplicar por 2 (calma... vamos por partes).

Passo 2

A gente usa a fórmula:

A = (1)/(2) int_(alpha)^(beta) [f (theta)]^2 d theta

Vamos primeiro naquele trechinho de 0 a (pi)/(6) que é onde as funções se encontram.

A_1 = (1)/(2) int_0^((pi)/(6)) (3 s e n theta)^2 d theta

A_1 = (1)/(2) int_0^((pi)/(6)) 9 s e n^2 theta d theta

A_1 = (1)/(2) [(9 theta)/(2) - 9 (s e n (2 theta))/(4)]_0^(pi // 6)

= (1)/(2) [(9 pi)/(12) - (9 sqrt(3))/(8)]

= (9 pi)/(24) - (9 sqrt(3))/(16)

Passo 3

Vamos agora pra área que vai desse ponto de interseção até o eixo y ...

A_2 = (1)/(2) int_((pi)/(6))^((pi)/(2)) ((3)/(2))^2 d theta

A_2 = (1)/(2) [(9)/(4) ((pi)/(2) - (pi)/(6))]

= (1)/(2) [(9)/(4) ((pi)/(3))]

= (9 pi)/(24)

Passo 4

Beleza, a soma dessas duas áreas dá a área da parte direita do gráfico, então pra acharmos a área total, é só a gente fazer:

A = 2 (A_1 + A_2)

A = 2 ((9 pi)/(24) - (9 sqrt(3))/(16) + (9 pi)/(24))

A = (3 pi)/(2) - (9 sqrt(3))/(8) u . a

Pronto! Essa é a área pedida😉

Resposta

A = (3 pi)/(2) - (9 sqrt(3))/(8) u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 1 a 36, faça um esboço do gráfico da equação dada 14. r = 4 - 3 s e n θ
Nos Exercícios de 1 a 36, faça um esboço do gráfico da equação dada 18. r = 6 + 2 c o s θ
Nos Exercícios de 1 a 36, faça um esboço do gráfico da equação dada 13. r = 2 - 3 s e n θ
Nos Exercícios de 1 a 36, faça um esboço do gráfico da equação dada 12. r = 3 + 3 c o s θ
Nos Exercícios de 1 a 36, faça um esboço do gráfico da equação dada 21. r = 2 c o s 4 θ