Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.6 - Ex. 13

13. Calcular ∬_R^() ( x + y ) d x d y onde R é a região delimitada por y = x^2 + 1 ; y = - 1 - x^2 ; x = - 1 e x = 1 .

Passo 1

Temos que a representação gráfica é a seguinte:

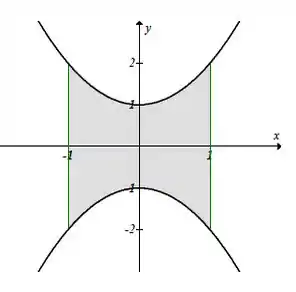
Seguindo a ordem de integração levando em consideração o gráfico, temos:

int_(- 1)^1 int_(- 1 - x^2)^(x^2 + 1) ( x + y ) d y d x

Vamos integrar em função de y e depois em função de x ,

int_(- 1 - x^2)^(x^2 + 1) ( x + y ) d y =

(x y + (y^2)/(2)|_(- 1 - x^2)^(x^2 + 1) = x (x^2 + 1) + ((x^2 + 1)^2)/(2) - x (- 1 - x^2) - ((- 1 - x^2)^2)/(2) =

= 2 x^3 + 2 x

Passo 2

int_(- 1)^1 (2 x^3 + 2 x) d x =

(((x^4)/(2) + x^2)|_(- 1)^1 = 0

Resposta

0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

23. Calcular ∬ R d xd y 1 - x + y onde R é a região descrita na figura 7.19.
22. Calcular ∬ R xd xd y onde R é a região descrita na figura 7.18.
21. Calcular ∬ R 1 + x + y d x d y onde R é delimitada pelo triângulo de vértices 1,1 , 1,2e2 , - 1 .
15. Calcular ∬ R ( x + 1 )d xd y , sendo R a região delimitada por x + y = 1 .