Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.11 - Ex. 29
Calcular
Onde S é a superfície plana , delimitada pelos planos , , ,
Passo 1
Podemos resolver esse exercício resolvendo a integral da seguinte maneia
Ou seja projetando a região no plano XY e parametrizando Z em função de X e Y
Primeiro vamos visualizar a região
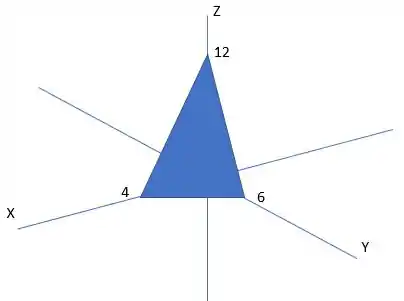
Esse é um recorte do plano
Se a gente projetar no plano XY, nossa equação de parametrização será
Mega fácil, certo?
Passo 2
Vamos dar uma olhada na nossa nova região
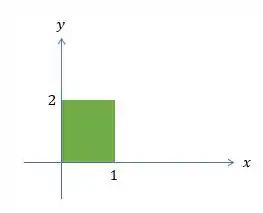
Como Temos vários planos cortando nossa região
Ao projetarmos no plano XY, obtemos um cubo. Logo nossa região de integração será
Passo 3
Vamos achar as derivadas parciais de z
Vamos agora montar nossa integral
Show! Vamos arregaçar as mangas e integrar
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Exercícios de Livros Relacionados
Determine a área da superfície.A parte da superfície z = x y que está dentro do cilindro x 2 + y 2 = 1 .
Determine a área da superfície.A parte do plano com equação vetorial r → u , v = 1 + v , u - 2 v ,3 - 5 u + v que é dada por 0 ≤ u ≤ 1 , 0 ≤ v ≤ 1 . ,
(a) Mostre que as equações paramétricas x = ac o s hu cos v, y = bc o s hus e nv, z = cs e n hu, representam um hiperboloide de uma folha.(b) Use as equações paramétricas da parte (a) para traçar o
Calcule a integral de superfície. ∫ ∫ Sx 2 z 2d S S é a parte do cone z 2 = x 2 + y 2 que está entre os planos z = 1 e z = 3
Calcule a integral de superfície. ∫ ∫ S( x 2 z + y 2 z )d S S é o hemisfério x 2 + y 2 + z 2 = 4, z ≥ 0