Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.6 - Ex. 18
18. Calcular , sendo a região delimitada por , .
Passo 1
Temos que a representação gráfica é a seguinte:
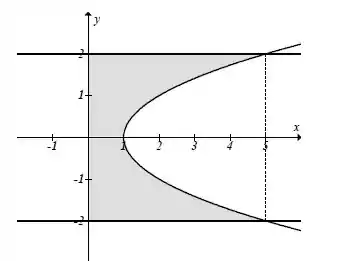
Analisando o gráfico, temos a seguinte integral:
Vamos integrar em relação a primeiro,
Passo 2
Resposta
Exercícios de Livros Relacionados
Desenhe o sólido limitado pelo plano x + y + z = 1 e pelo paraboloide z = 4 - x 2 - y 2 e determine seu volume exato. (Utilize seu SCA para fazer esse desenho, para achar as equações dos limites da re
Use a geometria ou simetria, ou ambas, para calcular a integral dupla. ∬ D a x 3 + b y 3 + a 2 - x 2 d A ,D = - a , a × - b , b
Use a geometria ou simetria, ou ambas, para calcular a integral dupla. ∬ D 2 + x 2 y 3 - y 2 sen x d A ,D = x , y | x + y ≤ 1
Use a geometria ou simetria, ou ambas, para calcular a integral dupla. ∬ D x + 2 d A ,D = x , y | 0 ≤ y ≤ 9 - x 2
Calcule a integrais iteradas.int_0^1 int_y^(2 - x) ( x^2 - y ) d y d x