Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 4.1 - Ex. 3f
Calcule:
Passo 1
A função módulo é definida por
Então podemos reescrever a integral, como a soma de 2 integrais
E ainda mais, se olharmos essa função graficamente
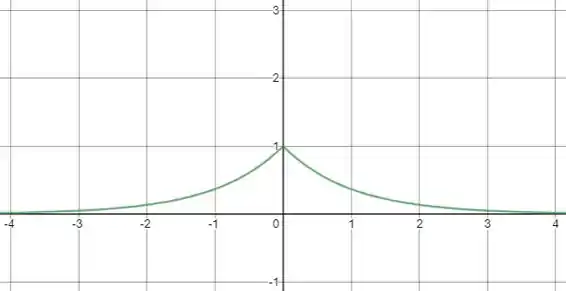
Podemos perceber a simetria da função, então é verdadeiro afirmar que
Logo
Passo 2
Vamos então calcular a integral
Como se trata de uma integral imprópria, a primeira coisa a se fazer é aplicar o limite
Agora podemos calcular a integral tranquilamente
Passo 3
Substituindo os limites de integração temos
Com a sua exponencial , logo a primeira fração vai para zero e temos que
Substituindo na primeira integral de nosso interesse
Resposta
Exercícios de Livros Relacionados
Utilize a integração, o teste da comparação direta ou o teste da comparação no limite para testar a integral quanto à convergência. Se mais de um método puder ser aplicado, use o de sua preferência. ∫
Utilize a integração, o teste da comparação direta ou o teste da comparação no limite para testar a integral quanto à convergência. Se mais de um método puder ser aplicado, use o de sua preferência. ∫
Utilize a integração, o teste da comparação direta ou o teste da comparação no limite para testar a integral quanto à convergência. Se mais de um método puder ser aplicado, use o de sua preferência. ∫
Utilize a integração, o teste da comparação direta ou o teste da comparação no limite para testar a integral quanto à convergência. Se mais de um método puder ser aplicado, use o de sua preferência. ∫
Utilize a integração, o teste da comparação direta ou o teste da comparação no limite para testar a integral quanto à convergência. Se mais de um método puder ser aplicado, use o de sua preferência. ∫