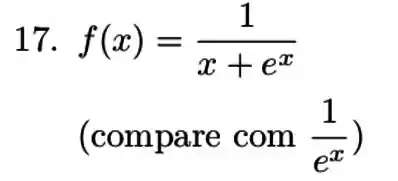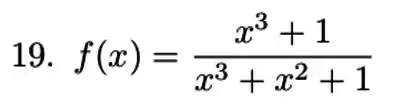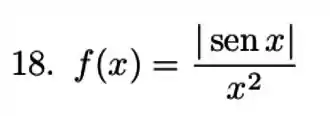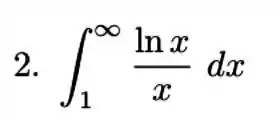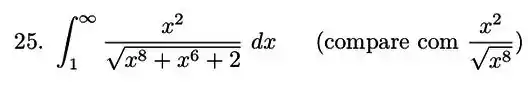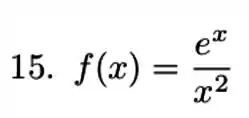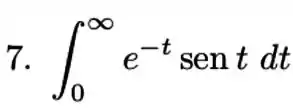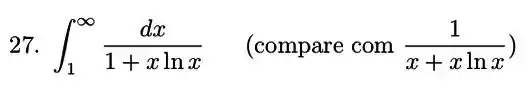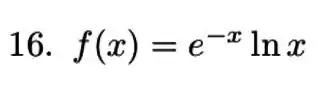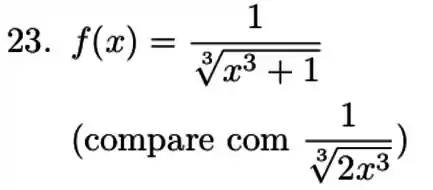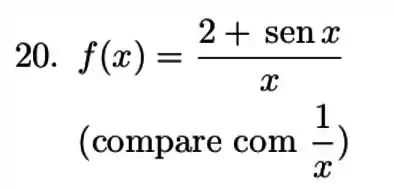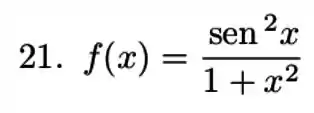Exercícios de Integrais Impróprias – Limites Sendo Infinito - Lista de Exercícios Resolvida

Analise a convergência da integral imprópria

Considere a região infinita limitada pela curva

e pelo eixo . Escreva uma integral que represente a área de e determine, sem calcular a integral, se essa região tem a área finita ou infinita. Justifique sua resposta.

Calcule:

Calcule a integral imprópria:

Verifique se a integral imprópria converge ou diverge:

Calcule as integrais abaixo utilizando integração por substituição simples.

(Capítulo 15.4 – Exercício 41) Utilize o resultado do Exercício , parte (c), para calcular as seguintes integrais:

(a)

(b)

Calcule:

Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes.

(e)

A velocidade média das moléculas em um gás ideal é dada por

Em que é o peso da molécula do gás, é a constante dos gases, é a temperatura do gás e é a velocidade molecular. Mostre que

Em cada item, determine a área da região .

1. e

Discuta a convergência da integral imprópria.

(Use integração por partes na e depois passe o limite quando )

Discuta a convergência da integral impropria

Nos exercícios a discuta a convergência da integral para a função dada.

Calcule as integrais

Calcule .

Determine se a integral diverge ou converge e, nesse último caso, calcule a integral:

Determine se a integral diverge ou converge e, nesse último caso, calcule a integral:

4a) Determine se a integral converge ou diverge, justificando sua resposta

Calcule a seguinte integral imprópria:

Calcule a integral

Considere as seguintes integrais impróprias

Analise a convergência de cada uma.

Verifique se a integral imprópria é convergente ou divergente. Caso seja convergente, calcule seu valor.

Questão 3)

b) Avalie a convergência da integral imprópria

e)

Avalie a integral:

4) Determine se a integral

É convergente ou divergente

Nos exercícios a use a definição para verificar se a integral imprópria converge ou diverge. Calcule o valor das integrais impróprias que convergem.

12)

Discuta a convergência de

Sugestão: Para , compare com ; para , calcule a integral; para , compare com

Nos exercícios a discuta a convergência das integrais impróprias.

Nos exercícios a discuta a convergência das integrais impróprias.

(discuta e use um teorema)

Calcule as integrais:

Calcule as integrais:

5. Determine o valor de tal que

Nos exercícios a discuta a convergência das integrais impróprias.

Calcule as integrais impróprias abaixo:

Determine para quais os valore de > 0 cada integral converge, e nesse caso, calcule a integral.

Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes.

(g)

Em cada item, para o qual a integral converge e determine o resultado da integral para esse valor de .

(a)

Calcule as seguintes integrais:

Calcule as integrais abaixo. Justifique as respostas.

Nos exercícios a use a definição para verificar se a integral imprópria converge ou diverge. Calcule o valor das integrais impróprias que converge.

8)

Avalie as integrais:

a)

b)

c)

d)

e)

f)

g)

Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes.

(h)

Avalie a convergência da integral imprópria.

Determine se a integral diverge ou converge e, nesse último caso, calcule a integral:

Q03a) Calcule a integral abaixo:

Q02a) Calcule a integral:

Avalie a convergência da integral imprópria

Em cada item, determine a área da região .

(b) e

Em cada item, para o qual a integral converge e determine o resultado da integral para esse valor de .

(b)

Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes.

(d)

Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes.

(f)

Calcule:

Resolva a integral:

Determine se as integrais abaixo são divergentes ou convergentes e calcule o valor daquelas que forem convergentes:

A integral imprópria

1. Convergente
2. Divergente

Calcule a integral:

Calcule o valor de

Nos exercícios 1 a 12 use a definição para verificar se a integral imprópria converge ou diverge. Calcule o valor das integrais impróprias que converge

4b) Calcule o valor de

Avalie se a integral imprópria

converge ou diverge. Se convergir, calcule o seu valor.

Avalie a convergência da integral imprópria

Discuta a convergência ou divergência da integral imprópria

Discuta a convergência ou divergência da integral imprópria

Determine se a seguinte integral imprópria é finita:

Calcule a seguinte integral imprópria

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

b)

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

a)

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

c)

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

g)

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

d)

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

e)

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

f)

Utilize o critério da comparação para decidir se cada integral converge ou diverge.

c)

10.3 Avalie a convergência da integral imprópria

Caso seja convergente, calcule seu valor.

Calcule as seguintes integrais:

Calcule de a ao longo da parábola .

7. Integrais impróprias

a)

7. Integrais impróprias

b)

EE3. 2012.2

EE3. 2011.2

EE3. 2008.2