Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.7 - Ex. 4b

Calcule a área de interseção da região limitada pelas curvas:

ρ = s e n θ

ρ = 1 - cos ⁡ θ

Passo 1

Primeiramente, vamos igualar as funções para descobrir o ponto de interseção entre elas:

s e n θ =   1 - cos ⁡ θ

1 = sen ( θ ) + c o s ⁡ ( θ )

Sabemos que os valores de θ = π 2   e     θ = 0 satisfazem a equação

Passo 2

Para facilitar a vizualização, vizualizaremos os gráficos superpostos.

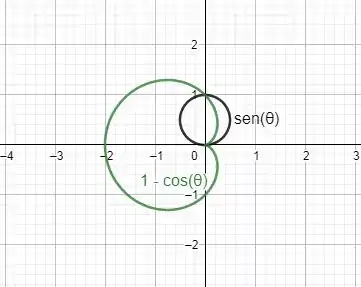
Podemos ver que a área entre as curvas é a área da curva verde de 0 até π 2 mais a área da curva preta de π 2 até π

Passo 3

Sabemos que a fórmula para a área em coordenadas polares é:

0,5 ∫ a b ρ ² d θ

Aplicando os limites de integração:

1 2 ∫ 0 π 2 1 - cos ⁡ θ 2 d θ + 1 2 ∫ π 2 π ( s e n ( θ ) ² d θ

0,5 ∫ 0 π 3 1 - cos ⁡ θ 2 d θ     =   0,5 ∫ 0 π 3 1 - 1 cos ⁡ θ +   c o s 2 θ d θ

Como cos²( θ ) = 1 2 + c o s 2 θ 2

0,5 ∫ 0 π 3 1 - 1 cos ⁡ θ +   c o s 2 θ d θ =     0,5 ∫ 0 π 3 1 - 1 cos ⁡ θ +   1 2 + c o s 2 θ 2 d θ = 3 π 8 - 2 2

Resolvendo a segunda parte:

1 2 ∫ π 2 π ( s e n ( θ ) ² d θ

Como sen²( θ ) = 1 2 - cos ⁡ 2 θ 2

1 2 ∫ π 2 π ( s e n ( θ ) ² d θ =   1 2 ∫ π 2 π 1 2 - cos ⁡ 2 θ 2 2 d θ = π 8

Logo, a área será

3 π 8 - 2 2 +   π 8 = π - 2 2

Resposta

A área vale π - 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Passe a curva para coordenadas polares e desenhe-a: x² + y² + x = ( x ² + y ² ) ² ²
Calcule a área da região dada (coordenadas polares): ρ = cos ⁡ 2 θ
3. Calcule a área limitada pela curva (coordenadas polares).d) ρ = cos ⁡ 3 θ
Escreva, em coordenadas polares, a equação da elipse x 2 a 2 + y 2 b 2 = 1 , tomando como pólo a origem e como eixo polar o semi-eixo Ox.
Calcule a área de interseção da região limitada pelas curvas: ρ = 1 ρ = 2 - 2 c o s ⁡ ( θ )