Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 7.4 - Ex. 8

Calcule a integral.

int (r^2)/(r + 4) d r

Passo 1

Opa! Vamos responder esse probleminha!! O enunciado pede pra a gente calcular a seguinte integral:

int (r^2)/(r + 4) d r

Pra isso vamos usar frações parciais na função:

(r^2)/(r + 4)

Aqui o numerador tem um grau maior que o denominador, então a gente precisa fazer uma divisão de polinômios. Vamos chamar o numerador de:

r^2 + r 0 + 0

Após isso, basta nos lembrarmos da seguinte relação:

D i v i d e n d o = D i v i s o r xx Q u o c i e n t e + R e s t o

Fazendo as continhas:

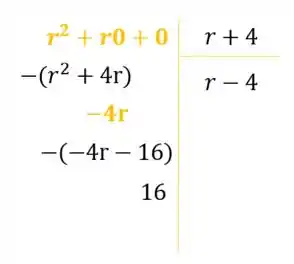
Podemos escrever da seguinte forma:

r^2 + r 0 + 0 = ( r + 4 ) (r - 4) + 16

Então:

(r^2)/(r + 4) = (r - 4) + (16)/(r + 4)

Passo 2

Substituindo na integral:

int (r^2)/(r + 4) d r = int r - 4 d r + int (16)/(r + 4) d r

int (r^2)/(r + 4) d r = int r d r - int 4 d r + int (16)/(r + 4) d r

Agora a única integral menos simples de resolver é:

int (16)/(r + 4) d r

Podemos fazer uma substituição, onde:

u = r + 4

(d u)/(d r) = 1 -> d u = d r

int (16)/(u) d u

Integrando:

int (16)/(u) d u = 16 ln u + C

Voltando a variável original:

16 ln u + C = 16 ln | r + u | + C

Agora vamos resolver as outras integrais:

int (r^2)/(r + 4) d r = int r d r - int 4 d r + 16 ln | r + u | + C

int (r^2)/(r + 4) d r = (r^2)/(2) - 4 r + 16 ln ( r + 4 ) + C

Prontinho!

Resposta

int (r^2)/(r + 4) d r = (r^2)/(2) - 4 r + 16 ln ( r + 4 ) + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a Integral.int (x^4 + 6 x^3 + 10 x^2 + x)/(x^2 + 6 x + 10) d x
Calcule a integral.int (2 x^2 - 2 x - 1)/(x^3 - x^2) d x
Calcule a integral.int (2 x^2 - 1)/(( 4 x - 1 ) ( x^2 + 1 )) d x
24. int (3 x^2 - x + 1)/(x^3 - x^2) d x
25. int (2 x^2 - 10 x + 4)/(( x + 1 ) ( x - 3 )^2) d x