Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 7.3 - Ex. 9

Calcule a integral.

int (d x)/(sqrt(x^2 + 16)) d x

Passo 1

Olá, meu nobre. Yuri aqui e estarei te ajudando a resolver esse problema.

Aqui vamos resolver essa integral indefinida. Para isso vamos utilizar de uma substituição trigonométrica, e a tabela abaixo eu creio que irá te ajudar.

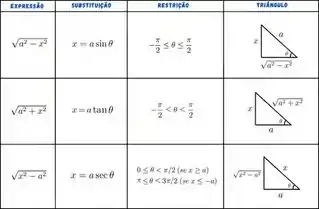
O triângulo retângulo associado a esse desenho é o seguinte:

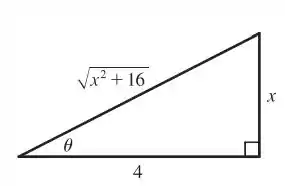
Passo 2

A gente tem que x = 4 tg theta , e theta varia no seguinte intervalo: - (pi)/(2) <= theta <= (pi)/(2) .

Assim, se fizermos a derivada de x , a gente tem d x = 4 sec^2 theta d theta .

Agora, achando o valor do nosso cateto sqrt(x^2 + 16) por meio da substituição de x , temos:

sqrt(x^2 + 16)

= sqrt((4 tg theta)^2 + 16)

= sqrt(16 tg^2 theta + 16)

= sqrt(16 (tg^2 theta - 1))

= sqrt(16 sec^2 theta)

= 4 |sec theta|

= 4 sec theta

para os valores relevantes de theta .

Passo 3

Assim, o valor da nossa integral é:

int (d x)/(sqrt(x^2 + 16)) d x = int (4 sec^2 theta d theta)/(4 sec theta)

= int sec theta d theta = ln | sec theta + tg theta | + C_1

Agora voltando para a variável original:

ln |(sqrt(x^2 + 16))/(4) + (x)/(4)| + C_1

= ln |sqrt(x^2 + 16) + x| - ln |4| + C_1

= ln ( sqrt(x^2 + 16) + x ) + C

Onde C = C_1 - ln 4 .

Como sqrt(x^2 + 16) + x > 0 , nós não precisamos do valor absoluto.

Resposta

ln ( sqrt(x^2 + 16) + x ) + C .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as integrais.
Calcule as integrais.
Calcule as integrais. A) Sem usar substituição trigonométrica
Calcule as integrais.
Calcule as integrais. B) Usando substituição trigonométrica