Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 7.3 - Ex. 25

Calcule a integral.

int (x)/(sqrt(x^2 + x + 1)) d x

Passo 1

Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa integral.

De cara a gente vê que essa integral é difícil de resolver por meios convencionais. Então para resolver essa atividade iremos manipular nossa função e iremos utilizar de substituições trigonométricas.

Para facilitar nosso cálculo, a gente faz essa transformação:

x^2 + x + 1 = (x^2 + x + (1)/(4)) + (3)/(4) = (x + (1)/(2))^2 + ((sqrt(3))/(2))^2

Além disso, iremos utilizar a tabela a seguir para nos ajudar a encontrar a substituição ideal:

Assim, a gente esboça a seguinte figura:

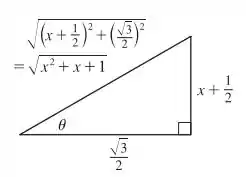
Passo 2

A gente tem que x + (1)/(2) = (sqrt(3))/(2) tg theta . Assim, se fizermos a derivada de x , a gente tem d x = (sqrt(3))/(2) sec^2 theta d theta e temos sqrt(x^2 + x + 1) = (sqrt(3))/(2) sec theta .

Passo 3

Assim, o valor da nossa integral é:

int (x)/(sqrt(x^2 + x + 1)) d x = int ((sqrt(3))/(2) tg theta - (1)/(2))/((sqrt(3))/(2) sec theta) (sqrt(3))/(2) sec^2 theta d theta

= int ((sqrt(3))/(2) tg theta - (1)/(2)) sec theta d theta

= int (sqrt(3))/(2) tg theta sec theta d theta - int (1)/(2) sec theta d theta

= (sqrt(3))/(2) sec theta - (1)/(2) ln |sec theta + tg theta| + C_1

= sqrt(x^2 + x + 1) - (1)/(2) ln |(2)/(sqrt(3)) sqrt(x^2 + x + 1) + (2)/(sqrt(3)) (x + (1)/(2))| + C_1

= sqrt(x^2 + x + 1) - (1)/(2) ln |(2)/(sqrt(3)) [sqrt(x^2 + x + 1) + (x + (1)/(2))]| + C_1

= sqrt(x^2 + x + 1) - (1)/(2) ln (2)/(sqrt(3)) - (1)/(2) ln (sqrt(x^2 + x + 1) + x + (1)/(2)) + C_1

= sqrt(x^2 + x + 1) - (1)/(2) ln (sqrt(x^2 + x + 1) + x + (1)/(2)) + C

Onde C = C_1 - (1)/(2) ln (2)/(sqrt(3)) .

Resposta

sqrt(x^2 + x + 1) - (1)/(2) ln (sqrt(x^2 + x + 1) + x + (1)/(2)) + C .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Com uma conveniente mudança de variével, transforme a integral dada numa do tipob) ∫ 3 x - 2 x 2 + x + 1 d x
Com uma conveniente mudança de variével, transforme a integral dada numa do tipob) ∫ x + 1 0 x 2 + 2 x + 2 d x
Calculem)int x ( a r c t g x ) ² d x ²
Calcule a integral int c o s 2 x c o s 6 x d x .
Calcule a integral.int sin^5 t cos^4 t d t