Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.8 - Ex. 21

Calcule a integral definida

int_(- 2)^5 | x - 3 | d x

Passo 1

Vamos lembrar de algumas Propriedades de integral

int_b^a f (x) d x = F (a) - F (b)

int_b^a f (x) + g (x) d x = int_b^a f (x) d x + int_b^a g (x) d x

int_()^() x^n = (x)/(n + 1)^(n + 1)

Passo 2

Tenho que contar um segredo. Ninguém gosta de calcular função com modulo. Então quando vemos um modulo, pensamos em como podemos quebrar ele.

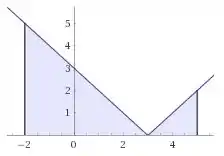
Por exemplo, observando o gráfico dessa função, vemos que para integrar temos como separar em 2 partes.Antes e depois do ponto de inflexão. Como a função é |x-3|. logo em x=3 é o ponto de inflexão.

Passo 3

Assim temos que a integral fica :

int_(- 2)^5 |x - 3| d x

= int_(- 2)^3 - ( x - 3 ) d x + int_3^5 x - 3 d x

Vamos integrar agora

((- (x^2)/(2) + 3 x)|_(x = - 2)^3 + (((x^2)/(2) - 3 x)|_(x = 3)^5

- (1)/(2) ( (3 )^2 - (- 2)^2) + 3 ( 3 - (- 2) ) + (1)/(2) (5^2 - 3^2) - 3 ( 5 - 3 )

= 29 // 2

Resposta

int_(- 2)^5 | x - 3 | d x = (29)/(2)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral. ∫ 1 4 y 2 - 4 y - 3 d y
Calcule a integral.int (1 + cos x)/(sen x) d x
Calcule a integral. ∫ 1 + x 1 - x d x
Calcule a integral.int (sqrt(2 x - 1))/(2 x + 3) d x
Calcule a integral.int_0^1 (1 + sqrt(x))^8 d x