Calcule a integral iterada.

onde é o sólido tetraedro com vértices , , , e .

Bom, nosso sólido é um tetraedro com vértices:

Vamos marcar esses pontos e desenhar o tetraedro:

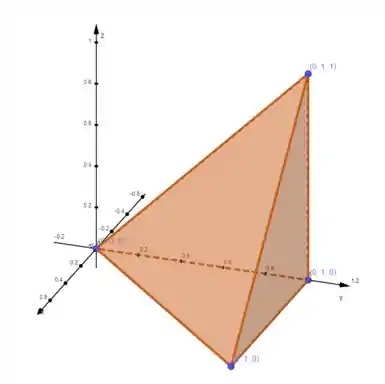
O nosso tetraedro está limitado por baixo pelo plano () e por cima pelo plano que contêm os pontos , e .

Vamos descobrir que plano é esse.

Um plano que passa por um ponto tem equação geral

Como ele passa pelo ponto :

A interseção desse plano com o plano () passa pelos pontos e , então é a reta:

Na nossa equação geral:

Como isso é a reta :

Voltando pra equação geral, vamos substituir o ponto :

Então o plano é

Isolando :

Como está entre e esse plano:

Para achar os limites de e , vamos ver a projeção do tetraedro no plano :

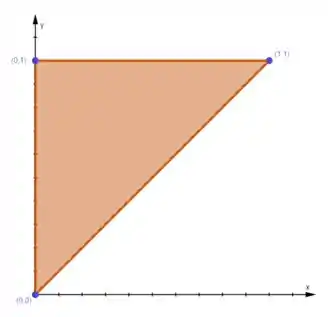
Nossa região está entre a reta e o eixo .

Para , isso significa que:

E o está entre e .

Assim, temos os limites de todas as variáveis:

Percebe que como os limites de dependem de e , temos que integrar em função de primeiro. Depois, como os limites de dependem de , depois vamos integrar em função de . Assim, a integral iterada fica:

Pra calcular essa integral, começamos integrando em função de , mantendo e como constantes:

Substituindo nos limites de integração:

Podemos tirar da integral, já que é constante, e abrir o quadrado da soma:

Agora, integramos em função de , considerando constante:

Aplicando nos limites de integração:

Colocando em evidência:

O que fica:

Por último, integramos em função de :

Calculando nos limites de integração:

Então: