Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.3 - Ex. 5h
Calcule.
Passo 1
Fala, galera! Tudo bem? Vamos resolver essa questão!
O enunciado pediu pra gente calcular o limite da função quando tende a .
Repare que substituir o valor na expressão, nos fornece uma inderterminação do tipo . Então, vamos tentar fatorar e simplificar a nossa expressão para fugir da indeterminação e aplicar o limite.
Vamo lá!
Passo 2
Vamos analisar o limite:
No numerador vamos tentar achar raízes, vamos usar o valor :
Dividindo por :
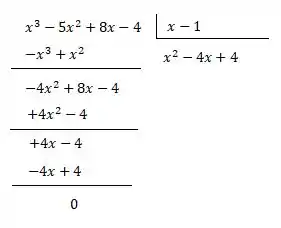
Vamos ter que:
Passo 3
Agora vamos analisar , vamos usar a seguinte fórmula para comparar e achar o valor de e :
De cara sabemos que , e temos que o termo:
Assim, temos que .
Vamos substituir:
Pronto, deu certinho, temos então que:
Passo 4
Para o denominador temos , vamos tentar achar raízes, vamos usar o valor :
Dividindo por :
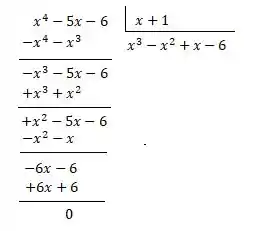
Vamos ter que:
Passo 5
Agora para , vamos tentar achar raízes, vamos usar o valor :
Dividindo por :
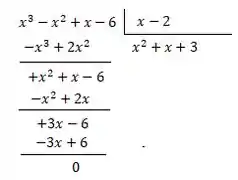
Vamos ter que:
Passo 6
Toda essa trabalheira, foi só pra gente poder escrever a nossa função fatorada no limite. Então, agora é só substituir no limite:
Simplificando:
Agora só é necessário substituir o valor na expressão, e achamos a resposta:
Valeu, galera! Até a próxima! 😉