Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 3.1 - Ex. 6d

Calcule int int_B f (x , y) d x d y sendo dados:

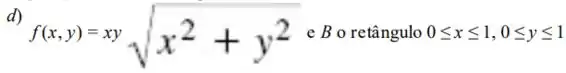
Passo 1

Chamando a integral dupla do teorema de Fubini de F :

F = int int_B f (x , y) d x d y

Podemos reescrevê-la como:

F = int int_B x y sqrt(x^2 + y^2) d x d y

Ou:

F = int_a^b [int_(c (y))^(d (y)) x y sqrt(x^2 + y^2) d x] d y = int_c^d [int_(a (x))^(b (x)) x y sqrt(x^2 + y^2) d y] d x

Como a figura em questão é um retângulo, sabe-se que o valor das variáveis variam de forma constante. Dessa forma, é possível resolver as integrais de forma direta por integrais definidas com os limites de integração dados por:

0 <= x <= 1

E

0 <= y <= 1

Passo 2

Assim, é possível calcular:

F = int_0^1 [int_(y = 0)^(y = 1) x y sqrt(x^2 + y^2) d y] d x

A integral interna pode ser resolvida através do método da substituição simples tomando u = x^2 + y^2 , tal que d u = 2 y d y . Então:

F = int_0^1 x [int_0^1 sqrt(u) ((d u)/(2))] d x

F = int_0^1 (x)/(2) [(2)/(3) u^(3 // 2)] | [[y,=,1],[y,=,0]] d x

Voltando para a variável original:

F = int_0^1 (x)/(3) [(x^2 + y^2)^(3 // 2)] | [[y,=,1],[y,=,0]] d x

Substituindo o intervalo de integração em y :

F = int_0^1 (x)/(3) [(x^2 + 1)^(3 // 2) - (x^2 + 0)^(3 // 2)] d x

F = (1)/(3) int_0^1 [x (x^2 + 1)^(3 // 2) - x^4] d x

Passo 3

Agora, para integrar em relação a x , a primeira parte pode ser resolvida através do método da substituição simples, com v = x^2 + 1 e d v = 2 x d x :

F = (1)/(3) {[int_0^1 [(v)^(3 // 2)] ((dv)/(2))] - [(x^5)/(5)] | [[x,=,1],[x,=,0]]}

F = (1)/(6) [(2)/(5) v^(5 // 2)] | [[x,=,1],[x,=,0]] - (1)/(15)

Voltando para a variável original:

F = (1)/(15) [(x^2 + 1)^(5 // 2)] | [[x,=,1],[x,=,0]] - (1)/(15)

E, substituindo o intervalo de integração:

F = (1)/(15) [(1 + 1)^(5 // 2) - (0 + 1)^(5 // 2)] - (1)/(15)

F = (1)/(15) [sqrt(32) - 1 - 1] = (1)/(15) [4 sqrt(2) - 2]

Ou:

F = (2)/(15) [2 sqrt(2) - 1]

Resposta

(2)/(15) [2 sqrt(2) - 1]

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = 3 - 2 x , y = x e
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = e - x , y = 1 e x
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = tg ⁡ x , x = 0 e
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = x 2 e y = x + 2 .
Nos Exercícios 19-24, esboce a região de integração e calcule a integral. ∫ 0 π ∫ 0 x x sen ⁡ y d yd x