Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 3.1 - Ex. 6l

Calcule int int_B f (x , y) d x d y sendo dados:

Passo 1

Chamando a integral dupla do teorema de Fubini de F :

F = int int_B f (x , y) d x d y

Podemos reescrevê-la como:

F = int int_B (x^5 c o s y^3) d x d y

Ou:

F = int_a^b [int_(c (y))^(d (y)) (x^5 c o s y^3) d x] d y = int_c^d [int_(a (x))^(b (x)) (x^5 c o s y^3) d y] d x

Fazendo o esboço do conjunto B , temos:

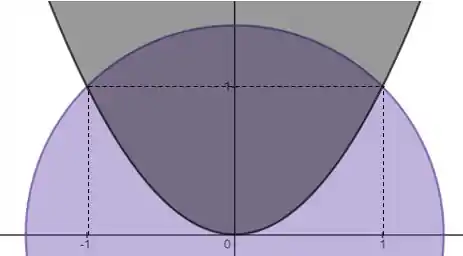
Através dos limites das variáveis dados pelo enunciado, pode-se tirar algumas conclusões sobre os valores de cada uma. Dessa forma, a partir da inequação da circunferência:

x <= +- sqrt(2 - y^2)

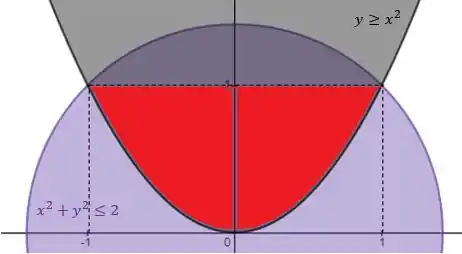
Assim, os intervalos serão:

0 <= y <= sqrt(2)

E

- sqrt(2 - y^2) <= x <= sqrt(2 - y^2)

Passo 2

Assim, é possível calcular:

F = int_0^(sqrt(2)) [int_(x = - sqrt(2 - y^2))^(x = sqrt(2 - y^2)) (x^5 c o s y^3) d x] d y

F = int_0^(sqrt(2)) c o s y^3 [(x^6)/(6)] | [[x,=,sqrt(2 - y^2)],[x,=,-,sqrt(2 - y^2)]] d y

Substituindo o intervalo de integração em x :

F = int_0^(sqrt(2)) (c o s y^3)/(6) [(sqrt(2 - y^2))^6 - (- sqrt(2 - y^2))^6] d y

F = int_0^(sqrt(2)) (c o s y^3)/(6) [(2 - y^2)^3 - (2 - y^2)^3] d y

F = 0

Resposta

0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as integrais iteradas. ∫ 0 2 ∫ y 2 y x yd xd y
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla.∬_D^() x d A , D = {(x , y)| 0 = x = pi , 0 = y = s e n x }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 v 1 - v 2 d ud v